Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao
Bài tập này thuộc chương trình học Đại số và Giải tích 11 Nâng cao, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến ... (nội dung cụ thể của câu 4).
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Giải các phương trình :
LG a
\({\sin ^4}x + {\cos ^4}x = {3 \over 4}\)
Lời giải chi tiết:
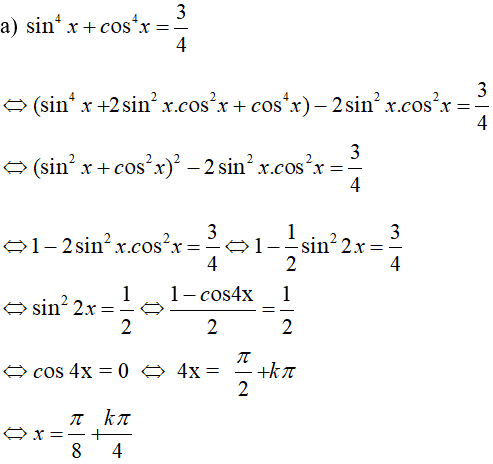
LG b
\({\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi \over 4}\)
Lời giải chi tiết:
\(\eqalign{ & {\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi \over 4} \cr & \Leftrightarrow 4{\sin ^2}x{\cos ^2}x - {\sin ^2}x = {1 \over 2} \cr & \Leftrightarrow 8{\sin ^2}x\left( {1 - {{\sin }^2}x} \right) - 2{\sin ^2}x = 1 \cr & \Leftrightarrow 8{\sin ^4}x - 6{\sin ^2}x + 1 = 0 \cr & \Leftrightarrow \left[ {\matrix{ {{{\sin }^2}x = {1 \over 2}} \cr {{{\sin }^2}x = {1 \over 4}} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {{{1 - \cos 2x} \over 2} = {1 \over 2}} \cr {{{1 - \cos 2x} \over 2} = {1 \over 4}} \cr } } \right. \cr & \Leftrightarrow \left[ {\matrix{ {\cos 2x = 0} \cr {\cos 2x = {1 \over 2}} \cr } } \right. \cr} \)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} + k\pi \\2x = \pm \frac{\pi }{3} + k2\pi \end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + \frac{{k\pi }}{2}\\x = \pm \frac{\pi }{6} + k\pi \end{array} \right.\)
LG c
\(\cos x\cos 2x = \cos 3x\)
Lời giải chi tiết:
\(\eqalign{ & \cos x\cos 2x = \cos 3x \cr & \Leftrightarrow {1 \over 2}\left( {\cos 3x + \cos x} \right) = \cos 3x \cr & \Leftrightarrow \cos 3x = \cos x \cr & \Leftrightarrow \left[ {\matrix{ {3x = x + k2\pi } \cr {3x = - x + k2\pi } \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = k\pi } \cr {x = k{\pi \over 2}} \cr } } \right.\cr& \Leftrightarrow x = k{\pi \over 2},k \in\mathbb Z \cr} \)
LG d
\(\tan 2x - \sin 2x + \cos 2x - 1 = 0\)
Lời giải chi tiết:
Điều kiện: \(\cos 2x \ne0\)
Ta có: \(\tan 2x = \dfrac{{\sin 2x}}{{\cos 2x}} \) \(\Rightarrow \sin 2x = \tan 2x\cos 2x\)
\(\eqalign{ & \tan 2x - \sin 2x + \cos 2x - 1 = 0 \cr & \Leftrightarrow \tan 2x - \tan 2x\cos 2x + \cos 2x - 1 = 0\cr & \Leftrightarrow \tan 2x\left( {1 - \cos 2x} \right) - \left( {1 - \cos 2x} \right) = 0 \cr & \Leftrightarrow \left( {1 - \cos 2x} \right)\left( {\tan 2x - 1} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{ {\tan 2x = 1} \cr {\cos 2x = 1} \cr } } \right. \cr} \)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{4} + k\pi \\2x = k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2}\\x = k\pi \end{array} \right.,k \in Z\)
Giải Chi Tiết Câu 4 Trang 223 SGK Đại số và Giải tích 11 Nâng cao
Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng, thường xuất hiện trong các đề thi và kiểm tra. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững kiến thức về ... (nội dung kiến thức liên quan). Dưới đây là lời giải chi tiết và các bước thực hiện:
Phân tích đề bài
Trước khi bắt đầu giải, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Đề bài yêu cầu ... (nêu lại yêu cầu của đề bài). Các dữ kiện quan trọng bao gồm ... (liệt kê các dữ kiện).
Lời giải chi tiết
Để giải quyết bài toán này, chúng ta sẽ sử dụng phương pháp ... (nêu phương pháp giải). Các bước thực hiện như sau:
- Bước 1: ... (mô tả bước 1).
- Bước 2: ... (mô tả bước 2).
- Bước 3: ... (mô tả bước 3).
- ...
Kết quả cuối cùng là ... (nêu kết quả cuối cùng).
Ví dụ minh họa
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
Giả sử ... (đưa ra một ví dụ cụ thể). Áp dụng các bước giải như trên, ta có thể tìm ra kết quả là ... (nêu kết quả của ví dụ).
Lưu ý quan trọng
- Khi giải bài tập này, cần chú ý đến ... (nêu các lưu ý quan trọng).
- Nên kiểm tra lại kết quả để đảm bảo tính chính xác.
- Thực hành thêm nhiều bài tập tương tự để nâng cao kỹ năng giải toán.
Mở rộng kiến thức
Kiến thức liên quan đến bài tập này còn được ứng dụng trong nhiều lĩnh vực khác, chẳng hạn như ... (nêu các ứng dụng). Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán phức tạp hơn trong tương lai.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
- Bài tập 1: ...
- Bài tập 2: ...
- ...
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao. Chúc bạn học tập tốt!
| STT | Nội dung | Giải thích |
|---|---|---|
| 1 | ... | ... |
| 2 | ... | ... |