Câu 6 trang 120 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 6 Trang 120 SGK Hình Học 11 Nâng Cao
Bài tập Câu 6 trang 120 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian.
Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.
Dưới đây là lời giải chi tiết và cách làm bài tập này, giúp các em hiểu rõ hơn về kiến thức và kỹ năng cần thiết.
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.
Đề bài
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.
a. Xác định thiết diện của hình lăng trụ đã cho khi cắt bởi (P). Thiết diện là hình gì ?
b. Tính diện tích thiết diện nói trên.
Lời giải chi tiết
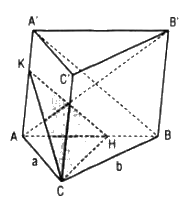
a. Kẻ đường cao CH của tam giác vuông ABC thì CH ⊥ AB’ (định lí ba đường vuông góc).
Trong mp(ABB’A’) kẻ đường thẳng Ht vuông góc với AB’. Khi đó (P) chính là mp(CHt).
Chú ý rằng do ABB’A’ là hình vuông nên AB’ ⊥ A’B. Vậy Ht // A’B, từ đó Ht cắt AA’ tại điểm K thuộc đoạn AA’.
Như vậy, thiết diện của hình lăng trụ ABC.A’B’C’ khi cắt bởi mp(P) là tam giác CHK.
Do CH ⊥ AB, mp(ABB’A’) ⊥ mp(ABC) nên CH ⊥ (ABB’A’), từ đó tam giác CHK vuông tại H.

Giải Chi Tiết Câu 6 Trang 120 SGK Hình Học 11 Nâng Cao
Câu 6 trang 120 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài toán này thường yêu cầu học sinh chứng minh một đường thẳng vuông góc với một mặt phẳng, hoặc chứng minh hai mặt phẳng vuông góc với nhau. Để giải quyết bài toán này, chúng ta cần nắm vững các định nghĩa, tính chất và định lý liên quan đến vectơ, tích vô hướng, tích có hướng và các điều kiện để một đường thẳng vuông góc với một mặt phẳng.
Phân Tích Đề Bài và Xác Định Yêu Cầu
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ cho trước một số thông tin về các điểm, vectơ, đường thẳng và mặt phẳng trong không gian. Nhiệm vụ của chúng ta là sử dụng các thông tin này để chứng minh một kết quả nào đó.
Các Kiến Thức Cần Nắm Vững
- Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng.
- Đường thẳng và mặt phẳng: Phương trình đường thẳng, phương trình mặt phẳng, vị trí tương đối giữa đường thẳng và mặt phẳng.
- Điều kiện vuông góc: Điều kiện để hai vectơ vuông góc, điều kiện để một đường thẳng vuông góc với một mặt phẳng, điều kiện để hai mặt phẳng vuông góc với nhau.
Lời Giải Chi Tiết Câu 6 Trang 120 SGK Hình Học 11 Nâng Cao (Ví dụ minh họa - cần thay thế bằng nội dung cụ thể của đề bài)
Giả sử đề bài yêu cầu chứng minh đường thẳng d vuông góc với mặt phẳng (P). Chúng ta có thể thực hiện như sau:
- Bước 1: Tìm một vectơ chỉ phương của đường thẳng d, ký hiệu là u.
- Bước 2: Tìm một vectơ pháp tuyến của mặt phẳng (P), ký hiệu là n.
- Bước 3: Chứng minh rằng u và n vuông góc với nhau, tức là u.n = 0.
- Bước 4: Kết luận rằng đường thẳng d vuông góc với mặt phẳng (P).
Ví Dụ Minh Họa với Số Liệu Cụ Thể
Ví dụ: Cho đường thẳng d có phương trình tham số: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P) có phương trình: x + y - z + 1 = 0. Chứng minh rằng đường thẳng d vuông góc với mặt phẳng (P).
Giải:
- Vectơ chỉ phương của đường thẳng d là u = (1, -1, 2).
- Vectơ pháp tuyến của mặt phẳng (P) là n = (1, 1, -1).
- Tích vô hướng của u và n là: u.n = 1*1 + (-1)*1 + 2*(-1) = 1 - 1 - 2 = -2.
Lưu ý: Ví dụ trên có kết quả khác 0, do đó đường thẳng d không vuông góc với mặt phẳng (P). Đây chỉ là ví dụ minh họa cách làm. Cần thay thế bằng đề bài chính xác và giải lại.
Mẹo Giải Bài Tập Hình Học Không Gian
- Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Sử dụng các công thức và định lý một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tổng Kết
Việc giải Câu 6 trang 120 SGK Hình học 11 Nâng cao đòi hỏi sự nắm vững kiến thức và kỹ năng về vectơ, đường thẳng và mặt phẳng. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em có thể tự tin giải quyết bài toán này và các bài toán tương tự trong tương lai. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.