Câu 13 trang 18 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 13 Trang 18 SGK Hình Học 11 Nâng Cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 13 trang 18 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học lớp 11, tập trung vào việc rèn luyện kỹ năng vận dụng kiến thức về vectơ và các phép toán vectơ.
Tusach.vn sẽ cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai tam giác vuông cân OAB
Đề bài
Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.
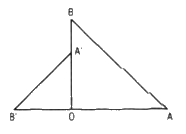
Lời giải chi tiết
Gọi Q là phép quay tâm O, góc quay \({\pi \over 2}\) (bằng góc lượng giác (OA ; OB)).
Khi đó Q:
+) biến O thành O
+) biến A thành B
+) biến A’ thành B’
Tức là Q biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG’\) và \(\widehat {GOG'} = {\pi \over 2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O
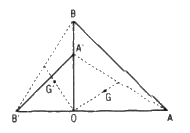
Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm của đoạn thẳng thành trung điểm đoạn thẳng.
Nghĩa là do phép quay Q biến AA' thành BB' thì biến trung điểm M của AA' thành trung điểm N của BB'.
Do đó Q biến OM thành ON. Khi đó Q biến G (thuộc OM) thành G' (thuộc ON) và \(OG' = OG = \frac{2}{3}OM = \frac{2}{3}ON\).
Vậy Q biến G thành G' là trọng tâm tam giác OBB'.
Giải Chi Tiết Câu 13 Trang 18 SGK Hình Học 11 Nâng Cao
Câu 13 trang 18 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ, đặc biệt là các phép toán cộng, trừ vectơ, nhân vectơ với một số thực và tích vô hướng của hai vectơ. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các định nghĩa, tính chất và công thức liên quan.
Nội Dung Bài Toán
Thông thường, dạng bài tập này sẽ yêu cầu chứng minh một đẳng thức vectơ, tìm một điểm thỏa mãn một điều kiện nào đó liên quan đến vectơ, hoặc tính độ dài của một vectơ. Ví dụ, bài toán có thể yêu cầu:
- Chứng minh rằng bốn điểm A, B, C, D thẳng hàng.
- Tìm điểm M sao cho MA + MB = 0.
- Tính AB.AC.
Phương Pháp Giải
Để giải quyết các bài toán về vectơ, chúng ta có thể áp dụng các phương pháp sau:
- Sử dụng tính chất của các phép toán vectơ: Ví dụ, AB + BC = AC.
- Biểu diễn vectơ qua các vectơ khác: Ví dụ, AM = k.AB.
- Sử dụng tích vô hướng:AB.AC = |AB| |AC| cos(AB, AC).
- Sử dụng hệ tọa độ: Gán tọa độ cho các điểm và thực hiện các phép toán vectơ trong hệ tọa độ.
Lời Giải Chi Tiết (Ví dụ minh họa - cần thay thế bằng lời giải cụ thể của câu 13 trang 18)
Giả sử câu 13 yêu cầu chứng minh rằng với tam giác ABC, nếu AB2 + AC2 = BC2 thì tam giác ABC vuông tại A.
Lời giải:
Ta có: BC2 = (AB + AC)2 = AB2 + 2AB.AC + AC2. Theo giả thiết, AB2 + AC2 = BC2, suy ra AB2 + AC2 = AB2 + 2AB.AC + AC2. Do đó, 2AB.AC = 0, tức là AB.AC = 0. Điều này có nghĩa là AB vuông góc với AC, hay tam giác ABC vuông tại A.
Lưu Ý Quan Trọng
Khi giải các bài toán về vectơ, cần chú ý:
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Sử dụng đúng các ký hiệu và thuật ngữ vectơ.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao. Ngoài ra, các em có thể tham khảo các bài giảng trực tuyến và các tài liệu học tập khác.
Tusach.vn - Đồng Hành Cùng Các Em
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Hình học 11 Nâng cao. Hãy truy cập tusach.vn để học tốt môn Hình học!
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |
| Bảng tóm tắt các khái niệm cơ bản. | |