Giải Câu 36 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 36 trang 68 SGK Hình học 11 Nâng cao

Giải Bài Tập Hình Học 11 Nâng Cao - Câu 36 Trang 68

Câu 36 trang 68 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết các vấn đề thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.

Đề bài

Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.

a. Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)

b. Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)

c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’khi cắt bởi mp(H , d)

Lời giải chi tiết

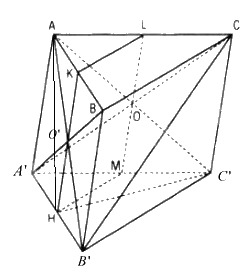
a) Chứng minh CB' // (AHC’)

Ta tìm trong (AHC’) một đường thẳng song song với CB’, muốn vậy ta tìm giao tuyến của (AHC’) với một mặt phẳng chứa CB’ và giao tuyến đó phải song song CB', đó là (A’B’C).

Dễ thấy \(H \in \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)

Gọi O là giao điểm AC’ và A’C nên

\(\left\{ \begin{array}{l}O \in AC' \subset \left( {AHC'} \right)\\O \in A'C \subset \left( {A'B'C} \right)\end{array} \right. \)\(\Rightarrow O \in \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)

Do đó \(OH = \left( {AHC'} \right) \cap \left( {A'B'C} \right)\)

AA’C’C là hình bình hành nên O là trung điểm của A’C.

Do đó HO là đường trung bình của ∆A’B’C

⇒ HO // B’C ⇒ B’C // (AHC’).

(vì HO \(\subset\) (AHC’)).

b) Tìm giao tuyến d của (AB’C’) và (A’BC).

Gọi O’ là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng (AB’C’) và (A’BC) nên (AB’C’) ∩ (A’BC) = OO’

Vậy d = OO’. Ta có O’ là trung điểm của AB’ ( vì AA’B’B là hình bình hành).

⇒ OO’ là đường trung bình của ∆AB’C’.

⇒ OO’ // B’C' // BC ⇒ OO’ // (BB’C’C) ⇒ d // (BB’C’C)

c) Gọi {K} = HO’ ∩ AB thì HK // AA’

Qua O kẻ ML // AA’ ( M ∈ A’C’, L ∈ AC).

Thiết diện cần tìm là hình bình hành HKLM.

Giải Chi Tiết Câu 36 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 36 trang 68 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ chỉ phương của đường thẳng, vectơ pháp tuyến của mặt phẳng, điều kiện song song, vuông góc, cắt nhau giữa đường thẳng và mặt phẳng.

Tóm Tắt Lý Thuyết Quan Trọng

Vectơ chỉ phương của đường thẳng: Một vectơ chỉ phương của đường thẳng là một vectơ song song với đường thẳng đó.
Vectơ pháp tuyến của mặt phẳng: Một vectơ pháp tuyến của mặt phẳng là một vectơ vuông góc với mọi vectơ nằm trong mặt phẳng đó.
Điều kiện song song: Đường thẳng song song với mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng vuông góc với vectơ pháp tuyến của mặt phẳng.
Điều kiện vuông góc: Đường thẳng vuông góc với mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng cùng phương với vectơ pháp tuyến của mặt phẳng.
Điều kiện cắt nhau: Đường thẳng cắt mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng không vuông góc với vectơ pháp tuyến của mặt phẳng.

Hướng Dẫn Giải Câu 36 Trang 68 (Ví dụ minh họa - cần thay đổi theo nội dung cụ thể của đề bài)

Giả sử câu 36 yêu cầu xác định góc giữa đường thẳng d và mặt phẳng (P). Các bước giải như sau:

Tìm vectơ chỉ phương của đường thẳng d: Ví dụ: a = (1, 2, 3)
Tìm vectơ pháp tuyến của mặt phẳng (P): Ví dụ: n = (4, 5, 6)
Tính cosin của góc giữa đường thẳng và mặt phẳng: Sử dụng công thức: cos(α) = |a.n| / (|a| * |n|), trong đó α là góc giữa đường thẳng và mặt phẳng.
Tính góc α:α = arccos(cos(α))

Các Dạng Bài Tập Liên Quan

Ngoài việc tính góc giữa đường thẳng và mặt phẳng, câu 36 và các bài tập tương tự có thể yêu cầu:

Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
Tìm hình chiếu của đường thẳng lên mặt phẳng.
Tìm giao điểm của đường thẳng và mặt phẳng.

Mẹo Giải Bài Tập Hình Học Không Gian

Để giải tốt các bài tập hình học không gian, bạn nên:

Vẽ hình minh họa để hình dung rõ hơn về bài toán.
Nắm vững các định nghĩa, tính chất và công thức liên quan.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm hình học để kiểm tra kết quả.

Luyện Tập Thêm

Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. tusach.vn cung cấp nhiều bài tập luyện tập và giải chi tiết để giúp bạn nâng cao kỹ năng giải toán.

Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải quyết Câu 36 trang 68 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các bạn học tốt!

Công thức	Mô tả
cos(α) = \|a.n\| / (\|a\| * \|n\|)	Cosin của góc giữa đường thẳng và mặt phẳng