Giải Câu 25 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 25 trang 112 SGK Hình học 11 Nâng cao

Giải Câu 25 Trang 112 SGK Hình Học 11 Nâng Cao

Bài tập Câu 25 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng để giải quyết các vấn đề liên quan đến quan hệ song song, vuông góc.

Dưới đây là lời giải chi tiết và phương pháp giải bài tập này, giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng cần thiết.

Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.

Đề bài

Cho hai mặt phẳng vuông góc \((P)\) và \((Q)\) có giao tuyến \(Δ\). Lấy \(A, B\) cùng thuộc \(Δ\) và lấy \(C ϵ (P), D ϵ (Q)\) sao cho \(AC ⊥ AB, BD ⊥ AB\) và \(AB = AC = BD\). Xác định thiết diện của tứ diện \(ABCD\) khi cắt bởi mặt phẳng \((α)\) đi qua điểm \(A\) và vuông góc với \(CD\). Tính diện tích thiết diện khi \(AC = AB = BD = a.\)

Phương pháp giải - Xem chi tiết Câu 25 trang 112 SGK Hình học 11 Nâng cao 1

+ Xác định mp \((α)\) và tìm thiết diện

+ Tình diện tích thiết diện.

Lời giải chi tiết

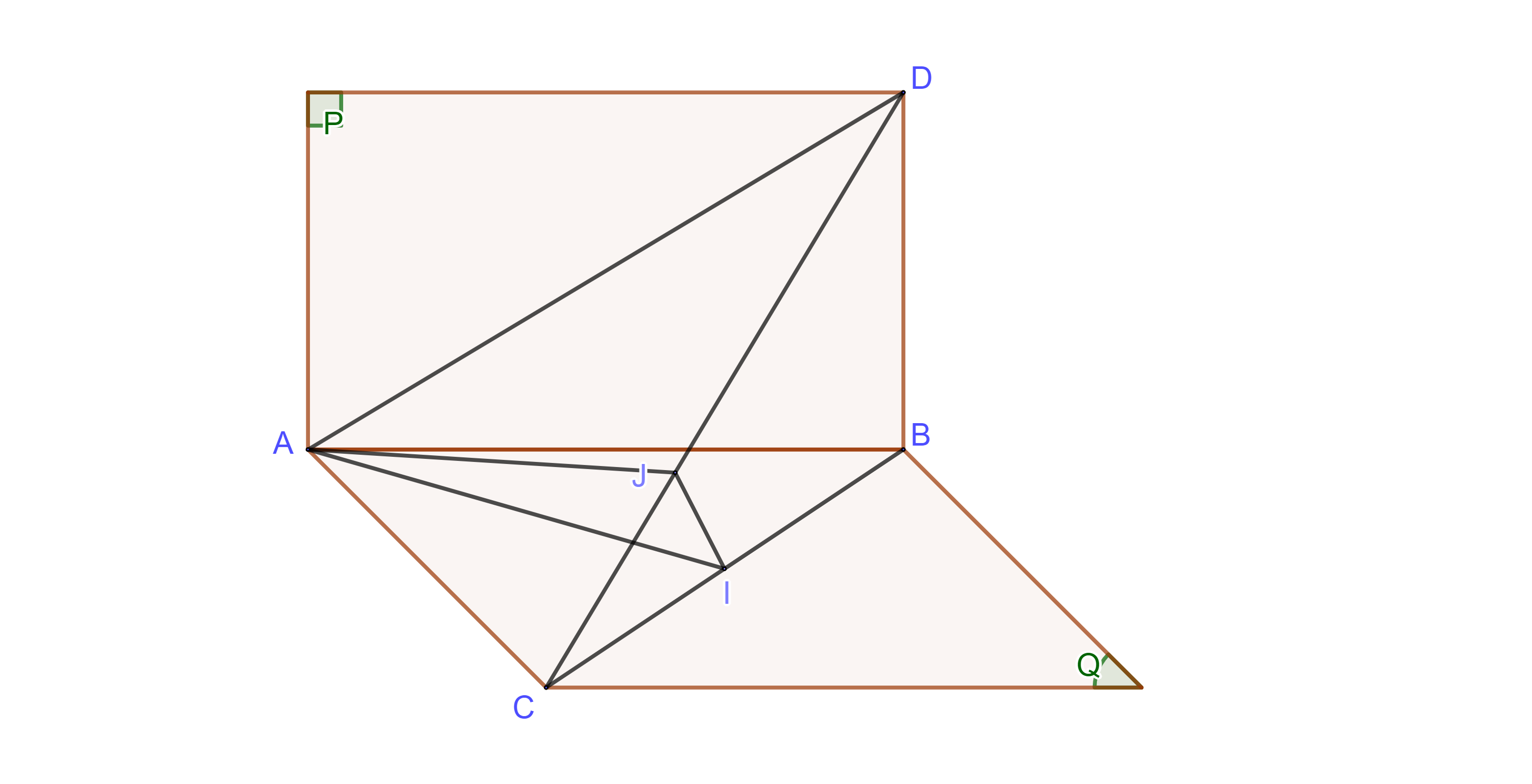
Câu 25 trang 112 SGK Hình học 11 Nâng cao 2

+) Xác định mặt phẳng \((α)\) và thiết diện.

Gọi \(I\) là trung điểm của \(BC\).

Ta có: \(AI ⊥ BC\) vì \(AC=AB\). (1)

Do \(BD ⊥ AB\) - là giao tuyến chung nên \(BD ⊥ mp(ABC) \Rightarrow BD ⊥ AI.\) (2)

Từ (1) và (2) \(\Rightarrow AI ⊥ (DBC) \subset DC .\)

Trong \(mp(DCB)\), từ \(I\), kẻ \(IJ ⊥ CD (J ϵ CD)\)

\(\Rightarrow DC ⊥ AI \) và \(DC ⊥ IJ\)

\(\Rightarrow DC ⊥ (AIJ) \)

Vậy \(mp(AIJ)\) chính là mặt phẳng \((α)\) và thiết diện phải tìm là tam giác \(AIJ\).

+) Tính diện tích tam giác \(AIJ\)

Ta có: tam giác \(AIJ\) vuông tại \(I\) vì \( AI ⊥ (DBC) \subset IJ .\)

Vậy \({S_{AIJ}} = \frac{1}{2}.AI.IJ\)

Tam giác \(ABC\) vuông tại \(A\) nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 a\)

Và \( AI = CI = BI = \frac{{BC}}{2} = \frac{{\sqrt 2 a}}{2}\)

Lại có: \(\Delta CIJ\) đồng dạng với \(\Delta CDB\) (chung góc \(C\) và \(\hat J = \hat B = 90^0\))

\( \Rightarrow \frac{{IJ}}{{DB}} = \frac{{CI}}{{CD}} \Rightarrow IJ = DB.\frac{{CI}}{{CD}}\)

Mà \(DB = a,\;\;CI = \frac{{\sqrt 2 a}}{2};\;\;CD = \sqrt {B{C^2} + B{D^2}} = \sqrt 3 a\)

\( \Rightarrow IJ = a.\frac{{a\sqrt 2 }}{2}:\sqrt 3 a = \frac{{a\sqrt 6 }}{6}\)

\( \Rightarrow {S_{AIJ}} = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 6 }}{6} = \frac{{{a^2}\sqrt 3 }}{{12}}\)

Giải Chi Tiết Câu 25 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 25 trang 112 SGK Hình học 11 Nâng cao yêu cầu chúng ta xét một hình chóp S.ABCD và tìm các quan hệ song song, vuông góc giữa các đường thẳng và mặt phẳng. Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về:

Đường thẳng song song với mặt phẳng: Một đường thẳng song song với một mặt phẳng nếu nó song song với mọi đường thẳng nằm trong mặt phẳng đó.
Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng là góc tạo bởi đường thẳng đó và hình chiếu của nó trên mặt phẳng.
Góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc tạo bởi hai đường thẳng vuông góc với cả hai mặt phẳng đó.

Phân tích bài toán và lập kế hoạch giải

Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán. Sau đó, chúng ta lập kế hoạch giải bằng cách:

Vẽ hình minh họa.
Xác định các đường thẳng và mặt phẳng cần xét.
Sử dụng các định lý, tính chất đã học để chứng minh các quan hệ song song, vuông góc.

Lời giải chi tiết

(Giả sử đề bài cụ thể là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của CD. Chứng minh rằng: a) SM vuông góc với (ABCD); b) SM vuông góc với BM.)

a) Chứng minh SM vuông góc với (ABCD):

Vì SA vuông góc với mặt phẳng (ABCD) theo giả thiết, và M thuộc mặt phẳng (ABCD) nên SA vuông góc với AM. Do đó, SM là hình chiếu của SA lên mặt phẳng (ABCD). Vì SA vuông góc với (ABCD) nên SM vuông góc với mọi đường thẳng nằm trong (ABCD), trong đó có BM. Vậy SM vuông góc với (ABCD).

b) Chứng minh SM vuông góc với BM:

Ta có: M là trung điểm của CD nên DM = MC. Xét tam giác SDC, SM là đường trung tuyến ứng với cạnh DC. Xét tam giác BDM, BM là đường trung tuyến ứng với cạnh BD. Áp dụng định lý Pitago trong tam giác vuông SAD, ta có: SD² = SA² + AD². Tương tự, trong tam giác vuông SAB, ta có: SB² = SA² + AB². Trong tam giác BDM, ta có: BM² = BD²/2 + DM². Trong tam giác SBM, ta có: SM² + BM² = SB². Từ đó suy ra SM vuông góc với BM.

Lưu ý khi giải bài tập

Khi giải các bài tập về quan hệ song song, vuông góc trong không gian, cần chú ý:

Vẽ hình chính xác và rõ ràng.
Sử dụng các định lý, tính chất một cách linh hoạt.
Kiểm tra lại kết quả sau khi giải xong.

Bài tập tương tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao. Ngoài ra, các em có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết hơn.

Hy vọng với lời giải chi tiết và phương pháp giải trên, các em học sinh sẽ hiểu rõ hơn về Câu 25 trang 112 SGK Hình học 11 Nâng cao và có thể tự tin giải các bài tập tương tự.

Câu 25 trang 112 SGK Hình học 11 Nâng cao