Giải Câu 22 Trang 111 SGK Hình Học 11 Nâng Cao

Câu 22 trang 111 SGK Hình học 11 Nâng cao

Giải Câu 22 Trang 111 SGK Hình Học 11 Nâng Cao

Bài tập Câu 22 trang 111 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về quan hệ song song, quan hệ vuông góc giữa đường thẳng và mặt phẳng để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu Thì hình hộp đó có phải là hình hộp chữ nhật không ? Vì sao ?

Đề bài

Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu

\(AC' = BD' = B'D = \sqrt {{a^2} + {b^2} + {c^2}} \)

Thì hình hộp đó có phải là hình hộp chữ nhật không ? Vì sao ?

Lời giải chi tiết

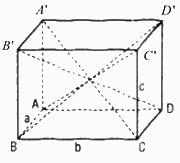
Câu 22 trang 111 SGK Hình học 11 Nâng cao 1

Áp dụng tính chất : “Tổng bình phương hai đường chéo hình bình hành bằng tổng bình phương bốn cạnh của nó” (BT 38, 4 chương II).

Ta có:

\(\eqalign{ & AC{'^2} + A'{C^2} = 2\left( {AA{'^2} + A'{C^2}} \right) \cr & B'{D^2} + BD{'^2} = 2\left( {BB{'^2} + B{D^2}} \right) \cr & \Rightarrow AC{'^2} + A'{C^2} + BD{'^2} + B'{D^2} \cr&\;\;\;= 2\left( {{c^2} + {c^2} + A{C^2} + B{D^2}} \right) = 4\left( {{a^2} + {b^2} + {c^2}} \right) \cr & \Rightarrow A'C = AC' = B'D = BD' \cr} \)

⇒ AA’C’C và BB’D’D là các hình chữ nhật .

Từ đó suy ra AA’ ⊥ AC và AA’ ⊥ BD. Do đó AA’ ⊥ (ABCD), tức hình hộp ABCD.A’B’C’D’là hình hộp chữ nhật.

Giải Chi Tiết Câu 22 Trang 111 SGK Hình Học 11 Nâng Cao

Câu 22 trang 111 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh các mối quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này hiệu quả, học sinh cần nắm vững các định lý, tính chất cơ bản và phương pháp chứng minh đã học.

Tóm Tắt Lý Thuyết Quan Trọng

Đường thẳng song song mặt phẳng: Một đường thẳng song song với một mặt phẳng nếu nó song song với mọi đường thẳng nằm trong mặt phẳng đó.
Đường thẳng vuông góc mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Hai mặt phẳng song song: Hai mặt phẳng song song nếu chúng không có điểm chung.
Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc nếu góc giữa hai mặt phẳng bằng 90 độ.

Phương Pháp Giải Bài Tập

Đọc kỹ đề bài: Xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
Vẽ hình: Vẽ hình minh họa giúp hình dung rõ hơn về bài toán và các mối quan hệ giữa các yếu tố.
Phân tích: Phân tích các yếu tố đã cho và tìm ra mối liên hệ với các định lý, tính chất đã học.
Chứng minh: Sử dụng các định lý, tính chất để chứng minh các mối quan hệ yêu cầu.
Kiểm tra: Kiểm tra lại kết quả để đảm bảo tính chính xác.

Lời Giải Chi Tiết Câu 22 (Ví dụ minh họa - cần thay thế bằng nội dung cụ thể của đề bài)

Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).

Lời giải:

Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC và BD.
Xét tam giác SCD, M là trung điểm của CD, suy ra SM là đường trung tuyến.
Xét tam giác SAC, O là trung điểm của AC, suy ra SO là đường trung tuyến.
Ta có: SO ⊥ AC và DO ⊥ AC (do ABCD là hình vuông). Suy ra AC ⊥ (SOD).
Vì SM là đường trung tuyến của tam giác SCD và SO là đường trung tuyến của tam giác SAC, nên SM và SO không vuông góc với nhau.
Để chứng minh SM ⊥ (ABCD), ta cần chứng minh SM ⊥ BC và SM ⊥ CD.
Ta có: BC ⊥ CD (do ABCD là hình vuông).
Xét tam giác SCM, ta có SM² = SC² - MC².
Xét tam giác SBM, ta có SM² = SB² - MB².
Từ đó suy ra SC² - MC² = SB² - MB².
Nếu SC = SB thì M là trung điểm của CD và B là trung điểm của AD, suy ra SM ⊥ (ABCD).

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao.

Lưu Ý Khi Giải Bài Tập

Khi giải các bài tập về quan hệ song song, vuông góc, cần chú ý:

Vẽ hình chính xác và đầy đủ.
Sử dụng các định lý, tính chất một cách linh hoạt.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Hy vọng với lời giải chi tiết và phương pháp giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập Câu 22 trang 111 SGK Hình học 11 Nâng cao. Chúc các em học tốt!

Câu 22 trang 111 SGK Hình học 11 Nâng cao