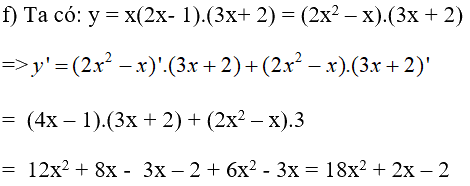Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao
SGK Toán 11 Nâng cao
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
CHƯƠNG V. ĐẠO HÀM
Bài 2. Các quy tắc tính đạo hàm

Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao

Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao

Bài tập Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các bài toán thực tế.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Tìm đạo hàm của mỗi hàm số sau :

LG aLG bLG cLG dLG eLG f

LG a

     \(y = \left( {{x^7} + {x}} \right)^2\)

    Phương pháp giải:

    Khai triển hằng đẳng thức và tính đạo hàm.

    Lời giải chi tiết:

    Ta có: \(y = {x^{14}} + 2{x^8} + {x^2} \) \(\Rightarrow y' = 14{x^{13}} + 16{x^7} + 2x\).

    Cách khác:

    Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

    LG b

      \(y = \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)\)

      Phương pháp giải:

      Sử dụng công thức đạo hàm của tích (uv)'=u'v+uv'

      Lời giải chi tiết:

      \(\eqalign{ & y' = \left( {{x^2} + 1} \right)'\left( {5 - 3{x^2}} \right) + \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)' \cr & = 2x\left( {5 - 3{x^2}} \right) - 6x\left( {{x^2} + 1} \right) \cr & = 10x - 6{x^3} - 6{x^3} - 6x\cr &= 4x - 12{x^3} \cr} \)

      LG c

        \(y = {{2x} \over {{x^2} - 1}}\)

        Phương pháp giải:

        Đạo hàm của thương \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)

        Lời giải chi tiết:

        \(y' \) \( = \frac{{\left( {2x} \right)'\left( {{x^2} - 1} \right) - 2x\left( {{x^2} - 1} \right)'}}{{{{\left( {{x^2} - 1} \right)}^2}}}\) \(= {{2\left( {{x^2} - 1} \right) - 2x\left( {2x} \right)} \over {{{\left( {{x^2} - 1} \right)}^2}}} \) \( = \frac{{ - 2{x^2} - 2}}{{{{\left( {{x^2} - 1} \right)}^2}}}\) \(= {{ - 2\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} - 1} \right)}^2}}}\)

        LG d

          \(y = {{5x - 3} \over {{x^2} + x + 1}}\)

          Lời giải chi tiết:

          Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

          \(y' = {{ - 5{x^2} + 6x + 8} \over {{{\left( {{x^2} + x + 1} \right)}^2}}}\)

          LG e

             \(y = {{{x^2} + 2x + 2} \over {x + 1}}\)

            Lời giải chi tiết:

            Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

            \(y' = {{{x^2} + 2x} \over {{{\left( {x + 1} \right)}^2}}}\)

            LG f

               \(y = x\left( {2x - 1} \right)\left( {3x + 2} \right)\)

              Lời giải chi tiết:

              Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

              \(\eqalign{ & y = 18{x^2} + 2x - 2 \cr} \)

              Giải Chi Tiết Câu 18 Trang 204 SGK Đại số và Giải tích 11 Nâng cao

              Câu 18 trang 204 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:

              • Định nghĩa hàm số đơn điệu: Hàm số f(x) được gọi là đơn điệu tăng trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≤ f(x2). Hàm số f(x) được gọi là đơn điệu giảm trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≥ f(x2).
              • Điều kiện để hàm số đơn điệu: Sử dụng đạo hàm để xét tính đơn điệu. Nếu f'(x) > 0 trên khoảng (a, b) thì hàm số f(x) đơn điệu tăng trên (a, b). Nếu f'(x) < 0 trên khoảng (a, b) thì hàm số f(x) đơn điệu giảm trên (a, b).
              • Các phương pháp tìm đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản và các quy tắc tính đạo hàm của hàm hợp.

              Ví dụ minh họa (giả định nội dung câu 18):

              Đề bài: Xét tính đơn điệu của hàm số y = x3 - 3x2 + 2.

              Giải:

              1. Tính đạo hàm: y' = 3x2 - 6x
              2. Tìm nghiệm của phương trình y' = 0: 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
              3. Xét dấu đạo hàm:
                x-∞02+∞
                y'+-+
                f(x)↗↘↗
              4. Kết luận: Hàm số y = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

              Mẹo giải nhanh và lưu ý

              • Luôn kiểm tra kỹ điều kiện xác định của hàm số trước khi tính đạo hàm.
              • Sử dụng bảng xét dấu đạo hàm để xác định khoảng đơn điệu một cách chính xác.
              • Chú ý đến các điểm không xác định của đạo hàm (ví dụ: điểm mà đạo hàm không tồn tại).

              Bài tập tương tự

              Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và sách bài tập. Tusach.vn sẽ cung cấp thêm các bài tập luyện tập và lời giải chi tiết trong các bài viết tiếp theo.

              Tusach.vn - Đồng hành cùng học sinh

              Tusach.vn là website học tập trực tuyến uy tín, cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập cho học sinh THPT. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong các kỳ thi!

              Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

              CHỦ ĐỀ SÁCH XEM NHIỀU

              Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

              VỀ TUSACH.VN