Câu 24 trang 23 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 24 Trang 23 SGK Hình Học 11 Nâng Cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 24 trang 23 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Tusach.vn sẽ cung cấp cho các em lời giải dễ hiểu, phương pháp giải khoa học và đáp án chính xác nhất.
Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau
Đề bài
Cho hai hình bình hành. Hãy vẽ một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau
Lời giải chi tiết
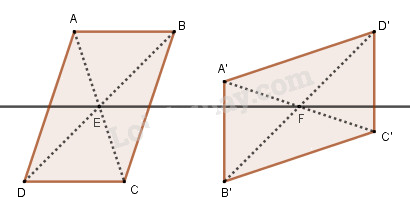
Một đường thẳng đi qua tâm O của hình bình hành thì chia hình bình hành đó thành hai phần bằng nhau, vì phép đối xứng qua tâm O sẽ biến phần này thành phần kia.
Bởi vậy, nếu cho hai hình bình hành, ta chỉ cần vẽ đường thẳng đi qua tâm của hai bình hành này thì đường thẳng đó sẽ chia mỗi hình bình hành thành hai phần bằng nhau.
Nếu tâm hai hình bình hành trùng nhau thì mọi đường thẳng đi qua tâm đó đều chia mỗi hình bình hành thành hai phần bằng nhau
Giải Chi Tiết Câu 24 Trang 23 SGK Hình Học 11 Nâng Cao
Câu 24 trang 23 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ trong không gian để chứng minh một đẳng thức vectơ. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ.
Đề Bài Câu 24 Trang 23 SGK Hình Học 11 Nâng Cao
Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của đoạn thẳng AC. Chứng minh rằng: overrightarrow{AI} = \frac{1}{2} \overrightarrow{AC}
Lời Giải Chi Tiết
Để chứng minh đẳng thức vectơ overrightarrow{AI} = \frac{1}{2} \overrightarrow{AC}, chúng ta cần phân tích mối quan hệ giữa các điểm A, I và C.
- Xác định vị trí điểm I: Đề bài cho biết I là trung điểm của đoạn thẳng AC. Điều này có nghĩa là I nằm trên đoạn AC và chia đoạn AC thành hai phần bằng nhau.
- Biểu diễn vectơ: Vì I là trung điểm của AC, ta có thể biểu diễn vectơ overrightarrow{AI} theo vectơ overrightarrow{AC}.
- Áp dụng định nghĩa trung điểm: Theo định nghĩa trung điểm, ta có: overrightarrow{AI} = \frac{1}{2} \overrightarrow{AC}.
Vậy, ta đã chứng minh được đẳng thức vectơ overrightarrow{AI} = \frac{1}{2} \overrightarrow{AC}.
Phương Pháp Giải Bài Toán Vectơ
Để giải các bài toán liên quan đến vectơ một cách hiệu quả, bạn nên làm theo các bước sau:
- Đọc kỹ đề bài: Xác định rõ các điểm, vectơ và mối quan hệ giữa chúng.
- Vẽ hình: Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Chọn hệ tọa độ: Nếu cần thiết, hãy chọn một hệ tọa độ phù hợp để biểu diễn các điểm và vectơ.
- Biểu diễn vectơ: Biểu diễn các vectơ theo các vectơ cơ sở hoặc các vectơ đã biết.
- Sử dụng các quy tắc và tính chất của vectơ: Áp dụng các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là hợp lý và phù hợp với điều kiện của bài toán.
Các Bài Tập Tương Tự
Để củng cố kiến thức về vectơ, bạn có thể luyện tập thêm các bài tập tương tự sau:
- Bài 1: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng overrightarrow{OA} = \frac{1}{2} \overrightarrow{AC}.
- Bài 2: Cho tam giác ABC. Gọi M là trung điểm của cạnh BC. Chứng minh rằng overrightarrow{AM} = \frac{1}{2} (\overrightarrow{AB} + \overrightarrow{AC}).
Kết Luận
Hy vọng rằng lời giải chi tiết và phương pháp giải bài tập vectơ trên sẽ giúp các em hiểu rõ hơn về Câu 24 trang 23 SGK Hình học 11 Nâng cao và tự tin hơn trong việc giải các bài toán tương tự. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Trung điểm | Điểm chia một đoạn thẳng thành hai phần bằng nhau. |