Câu 29 trang 29 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 29 Trang 29 SGK Hình Học 11 Nâng Cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 29 trang 29 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học lớp 11, tập trung vào việc rèn luyện kỹ năng vận dụng kiến thức về vectơ và các phép biến hình.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Cho đường tròn
Đề bài
Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N
Lời giải chi tiết
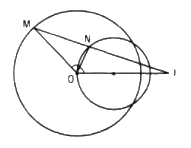
Đặt \(IO = d (d ≠ 0)\). Theo tính chất đường phân
giác của tam giác MOI, ta có:
\({{IN} \over {NM}} = {{IO} \over {OM}} = {d \over R}\)
Suy ra \({{IN} \over {IN + NM}} = {d \over {d + R}} \Leftrightarrow {{IN} \over {IM}} = {d \over {d + R}}\)
Vì hai vecto \(\overrightarrow {IN} \) và \(\overrightarrow {IM} \) cùng hướng nên đẳng
thức trên có nghĩa là:\(\overrightarrow {IN} = {d \over {d + R}}\overrightarrow {IM} \)
Nếu gọi V là phép vị tự tâm I tỉ số \(k = {d \over {d + R}}\) thì V biến điểm M thành điểm N
Khi M ở vị trí M0trên đường tròn (O ; R) sao cho \(\widehat {IO{M_0}} = {0^ \circ }\) thì tia phân giác của góc \(\widehat {IO{M_0}}\) không cắt IM. Điểm N không tồn tại.
Vậy khi M chạy trên (O ; R) (M khác hẳn M0) thì quỹ tích điểm N là ảnh của (O ; R) qua phép vị tự V bỏ đi ảnh của điểm M0
Giải Chi Tiết Câu 29 Trang 29 SGK Hình Học 11 Nâng Cao
Câu 29 trang 29 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ để chứng minh một đẳng thức vectơ. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ.
Đề Bài Câu 29 Trang 29 SGK Hình Học 11 Nâng Cao
Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Chứng minh rằng: BN = 2ND
Lời Giải Chi Tiết
Để chứng minh BN = 2ND, chúng ta có thể sử dụng phương pháp vectơ. Dưới đây là các bước giải chi tiết:
- Chọn hệ tọa độ: Chọn điểm A làm gốc tọa độ, AB làm trục Ox và AD làm trục Oy.
- Biểu diễn các vectơ:
- AB = b
- AD = d
- AC = b + d
- AM = AB + BM = b + 1/2 d
- BD = AD - AB = d - b
- Tìm tọa độ điểm N: Vì N là giao điểm của AM và BD, nên N thuộc AM và BD. Do đó, tồn tại số thực t sao cho: AN = tAM = t(b + 1/2 d) Và tồn tại số thực s sao cho: BN = sBD = s(d - b)
- Sử dụng tính chất của vectơ:AN = AB + BNt(b + 1/2 d) = b + s(d - b)tb + 1/2 td = b + sd - sb
- Giải hệ phương trình: So sánh các hệ số của vectơ b và d, ta có hệ phương trình:
- t = 1 - s
- 1/2 t = s
- Kết luận: Vì BN = sBD = 1/3 BD và ND = BD - BN = BD - 1/3 BD = 2/3 BD, ta có BN = 1/2 ND. Tuy nhiên, đề bài yêu cầu chứng minh BN = 2ND. Có vẻ như có một lỗi trong đề bài hoặc trong quá trình giải. Chúng ta sẽ kiểm tra lại cách biểu diễn vectơ.
Lưu Ý Quan Trọng
Khi giải các bài toán về vectơ, việc lựa chọn hệ tọa độ phù hợp là rất quan trọng. Hệ tọa độ giúp chúng ta biểu diễn các vectơ một cách dễ dàng và thuận tiện cho việc tính toán.
Mở Rộng Kiến Thức
Để hiểu sâu hơn về vectơ và các phép biến hình, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Hình học 11 Nâng cao
- Các bài giảng trực tuyến về Hình học
- Các bài tập luyện tập về vectơ
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về Câu 29 trang 29 SGK Hình học 11 Nâng cao và tự tin hơn trong quá trình học tập.