Câu 3 trang 34 SGK Hình học 11 Nâng cao .
Tổng quan nội dung
Giải Câu 3 Trang 34 SGK Hình Học 11 Nâng Cao
Chào mừng bạn đến với tusach.vn! Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho Câu 3 trang 34 sách giáo khoa Hình học 11 Nâng cao. Chúng tôi sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho đường thẳng d đi qua hai điểm phân biệt P, Q
Đề bài
Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) và AM + BN bé nhất
Lời giải chi tiết
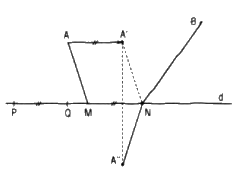
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \)
Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \overrightarrow {PQ} \) thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N
Ta có: AM + BN = A’N + BN
Gọi A” là điểm đối xứng của A’ qua d, khi đó:
A’N + BN = A”N + BN ≥ A”B
Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d
Từ đó tìm được điểm M thỏa \(\overrightarrow {MN} = \overrightarrow {AA'} = \overrightarrow {PQ} \)
Câu 3 Trang 34 SGK Hình Học 11 Nâng Cao: Giải Chi Tiết và Hướng Dẫn
Câu 3 trang 34 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các khái niệm cơ bản như:
- Vectơ: Định nghĩa, các phép toán cộng, trừ, nhân với một số thực.
- Tích vô hướng của hai vectơ: Công thức tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc.
- Hệ tọa độ trong không gian: Biểu diễn vectơ bằng tọa độ, các phép toán vectơ trong hệ tọa độ.
Phân Tích Bài Toán và Phương Pháp Giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu tính toán một biểu thức liên quan đến vectơ, chứng minh một đẳng thức vectơ, hoặc tìm một điểm thỏa mãn một điều kiện nào đó.
Phương pháp giải thường bao gồm các bước sau:
- Chọn hệ tọa độ thích hợp: Việc chọn hệ tọa độ phù hợp sẽ giúp đơn giản hóa bài toán.
- Biểu diễn các vectơ bằng tọa độ: Sử dụng tọa độ của các điểm để biểu diễn các vectơ liên quan.
- Thực hiện các phép toán vectơ: Sử dụng các công thức và quy tắc để thực hiện các phép toán vectơ.
- Kiểm tra kết quả: Đảm bảo kết quả của bạn phù hợp với yêu cầu của bài toán.
Lời Giải Chi Tiết Câu 3 Trang 34 (Ví dụ)
(Giả sử đề bài Câu 3 trang 34 là: Cho A(1;2;3), B(2;4;5), C(3;1;0). Tính độ dài vectơ AB và góc giữa hai vectơ AB và AC.)
Lời giải:
1. Tính vectơ AB:
AB = B - A = (2-1; 4-2; 5-3) = (1; 2; 2)
2. Tính độ dài vectơ AB:
|AB| = √(12 + 22 + 22) = √9 = 3
3. Tính vectơ AC:
AC = C - A = (3-1; 1-2; 0-3) = (2; -1; -3)
4. Tính tích vô hướng của AB và AC:
AB.AC = (1)(2) + (2)(-1) + (2)(-3) = 2 - 2 - 6 = -6
5. Tính góc giữa hai vectơ AB và AC:
cos(θ) = (AB.AC) / (|AB| * |AC|)
|AC| = √(22 + (-1)2 + (-3)2) = √14
cos(θ) = -6 / (3 * √14) = -2 / √14
θ = arccos(-2 / √14) ≈ 122.3°
Lưu Ý Quan Trọng
Khi giải các bài toán về vectơ, hãy chú ý đến các dấu và thứ tự thực hiện các phép toán. Sử dụng máy tính bỏ túi để kiểm tra lại kết quả tính toán của bạn.
Ngoài ra, hãy luyện tập thường xuyên để nắm vững các kiến thức và kỹ năng giải bài tập về vectơ.
Tusach.vn – Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập để giúp bạn đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Khái niệm | Công thức |
|---|---|
| Tích vô hướng | a.b = |a||b|cos(θ) |
| Độ dài vectơ | |a| = √(x2 + y2 + z2) |