Câu 3 trang 125 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 3 Trang 125 SGK Hình Học 11 Nâng Cao
Bài tập Câu 3 trang 125 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.
Đề bài
Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.
a. Xác định phép quay biến tam giác ABQ thành tam giác ANC.
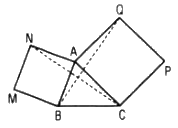
b. Chứng tỏ rằng hai đoạn thẳng BQ, CN bằng nhau và vuông góc với nhau.
c. Gọi O, O’ là tâm của các hình vuông, I là trung điểm của BC. Chứng minh rằng tam giác OIO’ là tam giác vuông cân.
Lời giải chi tiết
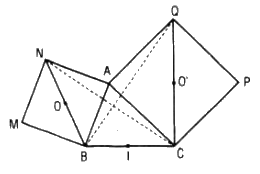
a. Ta có: AB = AN, AQ = AC và góc (AB, AN) bằng góc (AQ, AC) = -90˚
Vậy phép quay tâm A, góc quay φ = -90˚ biến tam giác ABQ thành tam giác ANC.
b. Vì đoạn thẳng BQ biến thành đoạn thẳng NC nên BQ = NC và BQ ⊥ NC.
c. Theo kí hiệu hình bên thì OI // NC, \(OI = {1 \over 2}NC;O'I//QB,O'I = {1 \over 2}BQ\)
vậy từ câu b ta suy ra tam giác IOO’ vuông cân tại đỉnh I.
Giải Chi Tiết Câu 3 Trang 125 SGK Hình Học 11 Nâng Cao
Câu 3 trang 125 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa các vectơ, đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
- Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng.
- Đường thẳng trong không gian: Phương trình tham số, phương trình chính tắc, vị trí tương đối giữa hai đường thẳng.
- Mặt phẳng trong không gian: Phương trình mặt phẳng, vị trí tương đối giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
Phân Tích Bài Toán và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải bài toán, hãy đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bài toán bằng cách:
- Vẽ hình: Vẽ hình minh họa bài toán để dễ dàng hình dung và tìm ra mối liên hệ giữa các yếu tố.
- Chọn hệ tọa độ: Chọn hệ tọa độ thích hợp để biểu diễn các điểm, vectơ, đường thẳng và mặt phẳng trong không gian.
- Sử dụng các công thức: Áp dụng các công thức và định lý đã học để giải bài toán.
Ví Dụ Minh Họa (Giả định một dạng bài tập phổ biến)
Đề bài: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Hãy tìm vectơ chỉ phương của đường thẳng AB.
Giải:
Vectơ chỉ phương của đường thẳng AB được tính bằng công thức:
AB = B - A = (3 - 1; 4 - 2; 5 - 3) = (2; 2; 2)
Vậy, vectơ chỉ phương của đường thẳng AB là (2; 2; 2).
Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải
Ngoài việc tìm vectơ chỉ phương, Câu 3 trang 125 SGK Hình học 11 Nâng cao còn có thể xuất hiện các dạng bài tập sau:
- Xác định vị trí tương đối giữa hai đường thẳng: Sử dụng tích có hướng của hai vectơ chỉ phương và một vectơ nối hai điểm trên hai đường thẳng.
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Sử dụng tích vô hướng của vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
- Tính góc giữa hai đường thẳng hoặc giữa đường thẳng và mặt phẳng: Sử dụng công thức tính góc dựa trên tích vô hướng hoặc tích có hướng.
Lưu Ý Quan Trọng
Khi giải các bài toán về hình học không gian, cần chú ý:
- Kiểm tra lại kết quả: Sau khi giải xong bài toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Sử dụng các công cụ hỗ trợ: Sử dụng máy tính hoặc phần mềm hình học để kiểm tra và minh họa kết quả.
- Luyện tập thường xuyên: Luyện tập thường xuyên các bài tập tương tự để nắm vững kiến thức và kỹ năng.
Kết Luận
Câu 3 trang 125 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian. Bằng cách nắm vững các kiến thức cơ bản, phân tích bài toán một cách cẩn thận và luyện tập thường xuyên, học sinh có thể giải quyết bài toán này một cách hiệu quả.
Chúc các em học tốt!