Giải Câu 28 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 28 trang 112 SGK Hình học 11 Nâng cao

Giải Câu 28 Trang 112 SGK Hình Học 11 Nâng Cao

Bài tập Câu 28 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về quan hệ song song, quan hệ vuông góc giữa đường thẳng và mặt phẳng để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng

LG a

Tam giác ABC có một cạnh song song hoặc nằm trong mp(P)

Lời giải chi tiết:

Xét trường hợp tam giác ABC có một cạnh, chẳng hạn BC nằm trong mp(P). Gọi A’ là hình chiếu của A trên mp(P).

Kẻ đường cao A’H của tam giác A’BC (H ϵ BC) thì AH là đường cao của tam giác ABC và \(\widehat {AHA'} = \varphi ,A'H = AH\cos \varphi .\)

Ta có: \({S_{A'BC}} = {1 \over 2}BC.A'H \) \(= {1 \over 2}BC.AH\cos \varphi = {S_{ABC.cos\varphi }}\)

Câu 28 trang 112 SGK Hình học 11 Nâng cao 1

Trường hợp cạnh BC của tam giác ABC song song với mp(P). Xét mp(Q) chứa BC và song song với mp(P), gọi giao điểm của AA’ với mp(Q) là A₁. Khi đó ta có ΔA₁BC = ΔA’B’C’ ; góc giữa mp(ABC) và mp(Q) bằng φ.

Do đó : \({S_{A'B'C'}} = {S_{{A_1}BC}} = {S_{ABC }.\cos \varphi}\)

LG b

Tam giác ABC không có cạnh nào song song hay nằm trong mp(P).

Lời giải chi tiết:

Câu 28 trang 112 SGK Hình học 11 Nâng cao 1

Xét trường hợp tam giác ABC không có cạnh nào song song hay nằm trong mp(P).

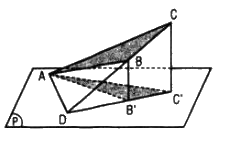
Ta có thể giả sử mp(P) đi qua điểm A sao cho các đỉnh B, C ở về cùng một phía đối với mp(P).

Gọi D là giao điểm của đường thẳng BC và mp(P); B’, C’ lần lượt là hình chiếu của B, C trên (P) thì B’C’ đi qua D.

Khi đó theo trường hợp a ta có :

\(\eqalign{ & {S_{ADC'}} = {S_{ADC.\cos \varphi }} \cr & {S_{ADB'}} = {S_{ABD.\cos \varphi }} \cr} \)

Trừ từng vế hai đẳng thức trên, ta có :

\({S_{AB'C'}} = {S_{ABC.\cos \varphi }}\)

Vậy mọi trường hợp ta đều có :

\({S_{A'B'C'}} = {S_{ABC.\cos \varphi }}\)

Giải Chi Tiết Câu 28 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 28 trang 112 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh các mối quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này hiệu quả, học sinh cần nắm vững các định lý, tính chất cơ bản về quan hệ giữa đường thẳng và mặt phẳng.

Tóm Tắt Lý Thuyết Quan Trọng

Đường thẳng song song với mặt phẳng: Một đường thẳng song song với một mặt phẳng nếu và chỉ nếu nó song song với một đường thẳng nào đó nằm trong mặt phẳng đó.
Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng nếu và chỉ nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Hai mặt phẳng song song: Hai mặt phẳng song song nếu chúng không có điểm chung.
Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc nếu góc giữa hai mặt phẳng bằng 90 độ.

Phân Tích Bài Toán Câu 28 Trang 112

Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Vẽ hình minh họa sẽ giúp bạn hình dung rõ hơn về không gian và các mối quan hệ giữa các yếu tố. Xác định các đường thẳng, mặt phẳng liên quan và các mối quan hệ cần chứng minh.

Lời Giải Chi Tiết (Ví dụ minh họa - cần thay thế bằng lời giải cụ thể của bài toán trong SGK)

Giả sử đề bài yêu cầu chứng minh đường thẳng d song song với mặt phẳng (P). Ta có thể thực hiện như sau:

Tìm một đường thẳng a nằm trong mặt phẳng (P) sao cho d song song với a.
Chứng minh d song song với a bằng cách sử dụng các định lý, tính chất đã học.
Kết luận d song song với mặt phẳng (P).

Các Dạng Bài Tập Liên Quan

Ngoài Câu 28, các bài tập về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng thường xuất hiện trong các đề thi. Một số dạng bài tập thường gặp bao gồm:

Chứng minh đường thẳng song song với mặt phẳng.
Chứng minh đường thẳng vuông góc với mặt phẳng.
Chứng minh hai mặt phẳng song song.
Chứng minh hai mặt phẳng vuông góc.
Tính góc giữa đường thẳng và mặt phẳng.
Tính góc giữa hai mặt phẳng.

Mẹo Giải Bài Tập Hình Học Không Gian

Để giải tốt các bài tập Hình học không gian, bạn nên:

Nắm vững các định lý, tính chất cơ bản.
Vẽ hình minh họa chính xác và rõ ràng.
Phân tích bài toán một cách logic và có hệ thống.
Sử dụng các phương pháp giải phù hợp.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Tài Liệu Tham Khảo Hữu Ích

Ngoài SGK, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Hình học:

Sách bài tập Hình học 11 nâng cao.
Các trang web học trực tuyến về Hình học.
Các video bài giảng về Hình học.

Tusach.vn hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải các bài tập về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng trong không gian. Chúc các em học tốt!

Câu 28 trang 112 SGK Hình học 11 Nâng cao