Giải Câu 19 Trang 204 SGK Đại số và Giải tích 11 Nâng cao

Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao

Giải Câu 19 Trang 204 SGK Đại số và Giải tích 11 Nâng cao

Bài tập Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Tìm đạo hàm của mỗi hàm số sau

LG a

\(y = {\left( {x - {x^2}} \right)^{32}}\)

Phương pháp giải:

Công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\)

Lời giải chi tiết:

y' = 32.(x- x²)³¹.(x - x²)'

= 32(x - x²)³¹.(1 - 2x)

Vậy \(y' = 32{\left( {x - {x^2}} \right)^{31}}\left( {1 - 2x} \right)\)

LG b

\(y = {1 \over {x\sqrt x }}\)

Phương pháp giải:

Sử dụng công thức \(\left( {\frac{1}{u}} \right)' = \frac{{ - u'}}{{{u^2}}}\)

Lời giải chi tiết:

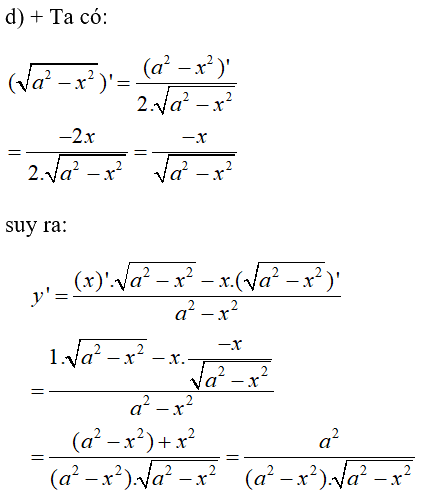
Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

\( \Rightarrow \left( {\frac{1}{{x\sqrt x }}} \right)' = \frac{{ - \left( {x\sqrt x } \right)'}}{{{{\left( {x\sqrt x } \right)}^2}}} \) \(= \frac{{ - \frac{{3\sqrt x }}{2}}}{{{x^2}.x}} = - \frac{3}{{2{x^2}\sqrt x }}\)

\(y' = {{ - 3} \over {2{x^2}\sqrt x }}\)

LG c

\(y = {{1 + x} \over {\sqrt {1 - x} }}\)

Phương pháp giải:

Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)

Lời giải chi tiết:

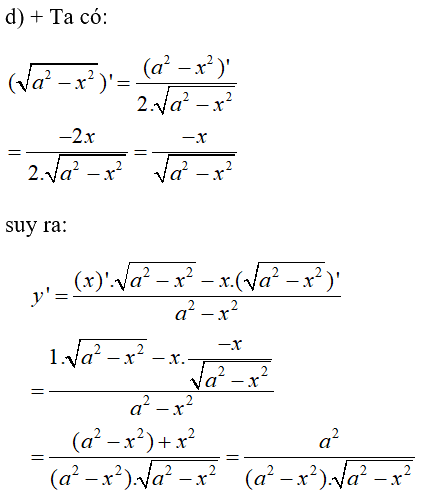
Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

\(y' = {{3 - x} \over {2\sqrt {{{\left( {1 - x} \right)}^3}} }}\)

LG d

\(y = {x \over {\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)

Phương pháp giải:

Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).

Lời giải chi tiết:

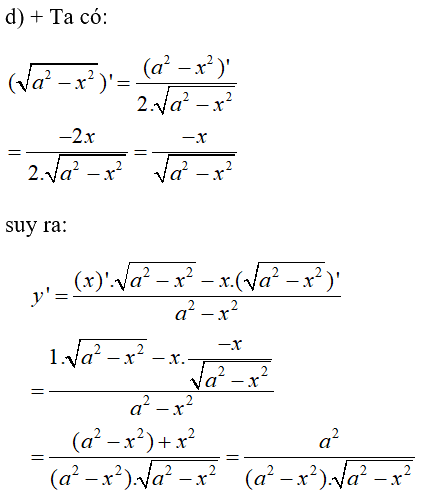
Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao 1

\(\eqalign{ & y' = {{{a^2}} \over {\sqrt {{{\left( {{a^2} - {x^2}} \right)}^3}} }} \cr} \)

Giải Chi Tiết Câu 19 Trang 204 SGK Đại số và Giải tích 11 Nâng cao

Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến việc xét tính đơn điệu của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:

Định nghĩa hàm số đơn điệu: Hàm số f(x) được gọi là đồng biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≤ f(x2). Hàm số f(x) được gọi là nghịch biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≥ f(x2).
Điều kiện để hàm số đơn điệu:
- Nếu f'(x) > 0 với mọi x thuộc khoảng (a, b) thì hàm số f(x) đồng biến trên (a, b).
- Nếu f'(x) < 0 với mọi x thuộc khoảng (a, b) thì hàm số f(x) nghịch biến trên (a, b).
Cách tìm đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit) và quy tắc tính đạo hàm của hàm hợp.

Ví dụ minh họa (giả định nội dung câu 19):

Đề bài: Xét tính đơn điệu của hàm số f(x) = x³ - 3x² + 2.

Giải:

Tính đạo hàm: f'(x) = 3x² - 6x.
Tìm nghiệm của f'(x) = 0: 3x² - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
Xét dấu f'(x):
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Kết luận: Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Mẹo giải nhanh và hiệu quả

Để giải nhanh các bài toán xét tính đơn điệu, bạn nên:

Tính đạo hàm một cách chính xác.
Tìm nghiệm của phương trình đạo hàm bằng 0.
Lập bảng xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến.
Chú ý đến tập xác định của hàm số.

Bài tập tương tự

Để luyện tập thêm, bạn có thể tham khảo các bài tập tương tự sau:

Câu 20 trang 204 SGK Đại số và Giải tích 11 Nâng cao
Bài tập 1.5 trang 15 SBT Đại số và Giải tích 11 Nâng cao

Tổng kết

Việc nắm vững kiến thức về đạo hàm và tính đơn điệu của hàm số là rất quan trọng trong chương trình Đại số và Giải tích 11 Nâng cao. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em học sinh sẽ tự tin hơn khi giải quyết các bài tập liên quan.

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi tại tusach.vn. Chúng tôi luôn sẵn sàng hỗ trợ bạn!

Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao