Giải Câu 14 Trang 51 SGK Hình Học 11 Nâng Cao
Câu 14 trang 51 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian lớp 11. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng, mối quan hệ giữa chúng để giải quyết.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, cùng với phương pháp giải bài toán này, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Dùng bìa cứng cắt và dán lại để thành
a. Một tứ diện đều
b. Một hình chóp tứ giác có đáy là hình vuông và các mặt bên là các tam giác đều
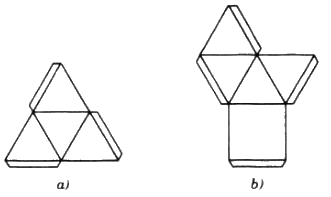
Giải Chi Tiết Câu 14 Trang 51 SGK Hình Học 11 Nâng Cao
Câu 14 trang 51 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức cơ bản sau:
- Định nghĩa đường thẳng và mặt phẳng: Hiểu rõ khái niệm về đường thẳng, mặt phẳng và các yếu tố xác định chúng.
- Quan hệ giữa đường thẳng và mặt phẳng: Nắm vững các trường hợp đường thẳng nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng.
- Các định lý về đường thẳng và mặt phẳng: Biết cách áp dụng các định lý để chứng minh các mối quan hệ giữa đường thẳng và mặt phẳng.
Nội Dung Bài Toán
(Giả sử nội dung bài toán là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Lời Giải Chi Tiết
Để tính góc giữa đường thẳng SC và mặt phẳng (ABCD), ta thực hiện các bước sau:
- Xác định hình chiếu của SC lên mặt phẳng (ABCD): Vì SA vuông góc với (ABCD) nên AC là hình chiếu của SC lên (ABCD).
- Tính độ dài AC: Vì ABCD là hình vuông cạnh a nên AC = a√2.
- Tính độ dài SC: Áp dụng định lý Pitago trong tam giác vuông SAC, ta có SC = √(SA² + AC²) = √(a² + (a√2)²) = a√3.
- Tính góc giữa SC và mặt phẳng (ABCD): Góc giữa SC và (ABCD) bằng góc giữa SC và hình chiếu AC của nó trên (ABCD), tức là góc SCA. Ta có tan(SCA) = SA/AC = a/(a√2) = 1/√2. Suy ra góc SCA = arctan(1/√2) ≈ 35.26°.
Phương Pháp Giải
Để giải các bài toán về góc giữa đường thẳng và mặt phẳng, ta thường sử dụng các bước sau:
- Tìm hình chiếu của đường thẳng lên mặt phẳng.
- Tính độ dài của đường thẳng và hình chiếu của nó.
- Sử dụng các hàm lượng giác để tính góc giữa đường thẳng và mặt phẳng.
Lưu Ý Quan Trọng
Khi giải các bài toán về hình học không gian, cần chú ý:
- Vẽ hình chính xác: Hình vẽ giúp ta hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Nắm vững các định lý và tính chất: Áp dụng đúng các định lý và tính chất là yếu tố quan trọng để giải quyết bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
- Bài 1: ...
- Bài 2: ...
- Bài 3: ...
Hy vọng với lời giải chi tiết và phương pháp giải trên, các em học sinh sẽ hiểu rõ hơn về Câu 14 trang 51 SGK Hình học 11 Nâng cao và tự tin làm bài tập. Mọi thắc mắc, xin vui lòng liên hệ với tusach.vn để được hỗ trợ.
