Giải Câu 20 Trang 114 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao

Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về hàm số, đạo hàm, hoặc các chủ đề khác đã được học để giải quyết một vấn đề cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.

Trên tia Ox

Đề bài

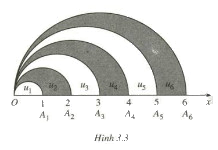
Trên tia Ox lấy các điểm A₁, A₂, …, A_n, … sao cho với mỗi số nguyên dương n, OA_n = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OA_n, n = 1, 2, … . Kí hiệu u₁ là diện tích của nửa hình tròn đường kính OA₁ và với mỗi n ≥ 2, kí hiệu u_n là diện tích của hình giới hạn bởi nửa đường tròn đường kính OA_{n – 1}, nửa đường tròn đường kính OA_n và tia Ox (h 3.3). Chứng minh rằng dãy số (u_n) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.

Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao 1

Lời giải chi tiết

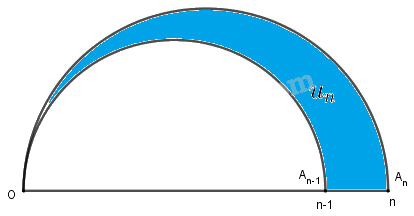
Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao 2

Với \(n ≥ 2\) ta có :

Diện tích nửa đường tròn đường kính \(OA_n\) là: \({S_n} = \frac{1}{2}\pi .{\left( {\frac{{O{A_n}}}{2}} \right)^2} = \frac{1}{8}\pi {n^2}\)

Diện tích nửa đường tròn đường kính \(OA_{n-1}\) là: \({S_{n-1}} = \frac{1}{2}\pi .{\left( {\frac{{O{A_{n-1}}}}{2}} \right)^2} = \frac{1}{8}\pi {(n-1)^2}\)

Do đó,

\(\eqalign{& {u_n} ={S_n} - {S_{n-1}}\cr& = \frac{1}{8}\pi {n^2} - \frac{1}{8}\pi {\left( {n - 1} \right)^2} \cr & = {1 \over 8}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right] \cr & = \frac{1}{8}\pi \left( {{n^2} - {n^2} + 2n - 1} \right)\cr&= {{\left( {2n - 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr & \Rightarrow {u_{n + 1}} - {u_n} \cr&= {{2n + 1} \over 8}\pi - {{\left( {2n - 1} \right)} \over 8}\pi \cr&= {\pi \over 4},\forall n \ge 2 \cr} \)

Mặt khác

\({u_2} - {u_1} = {{3\pi } \over 8} - {\pi \over 8} = {\pi \over 4}\)

Vậy \({u_{n + 1}} - {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)

Do đó (u_n) là cấp số cộng với công sai \(d = {\pi \over 4}.\)

Giải Chi Tiết Câu 20 Trang 114 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao thường thuộc các dạng bài tập về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến giới hạn. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản và kỹ năng giải toán.

Phân Tích Đề Bài và Xác Định Yêu Cầu

Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn tránh sai sót và tìm ra phương pháp giải phù hợp. Ví dụ, đề bài có thể yêu cầu tính đạo hàm của một hàm số, tìm cực trị của hàm số, hoặc giải phương trình chứa đạo hàm.

Các Bước Giải Bài Tập (Ví dụ minh họa - Giả sử đề bài yêu cầu tìm đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1)

Bước 1: Xác định quy tắc đạo hàm cần sử dụng. Trong trường hợp này, chúng ta sẽ sử dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa: (u ± v)' = u' ± v' và (x^n)' = nx^(n-1).
Bước 2: Áp dụng quy tắc đạo hàm cho từng thành phần của hàm số.
- (x^3)' = 3x^2
- (-2x^2)' = -4x
- (5x)' = 5
- (-1)' = 0
Bước 3: Kết hợp các kết quả để tìm đạo hàm của hàm số f(x).
f'(x) = 3x^2 - 4x + 5

Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải

Bài tập về đạo hàm của hàm số đơn thức và đa thức: Sử dụng quy tắc đạo hàm của lũy thừa và các quy tắc cộng, trừ, nhân, chia.
Bài tập về đạo hàm của hàm hợp: Sử dụng quy tắc đạo hàm của hàm hợp: (f(g(x)))' = f'(g(x)) * g'(x).
Bài tập về đạo hàm của hàm lượng giác: Nắm vững các công thức đạo hàm của các hàm lượng giác cơ bản (sin x, cos x, tan x, cot x).
Bài tập về ứng dụng đạo hàm để khảo sát hàm số: Tìm cực trị, điểm uốn, khoảng đồng biến, nghịch biến của hàm số.

Lưu Ý Quan Trọng Khi Giải Bài Tập

Để giải bài tập một cách chính xác và hiệu quả, bạn cần:

Nắm vững các định nghĩa, định lý và công thức liên quan.
Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Kiểm tra lại kết quả sau khi giải xong.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán khi cần thiết.

Tusach.vn - Nguồn Tài Liệu Học Tập Toán Học Uy Tín

tusach.vn là một website cung cấp đầy đủ các tài liệu học tập toán học, bao gồm sách giáo khoa, sách bài tập, đề thi, và lời giải chi tiết. Chúng tôi cam kết cung cấp cho bạn những thông tin chính xác, hữu ích và cập nhật nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Ví dụ minh họa khác (Bài tập về ứng dụng đạo hàm để tìm cực trị):

Giả sử hàm số y = x^3 - 3x^2 + 2. Để tìm cực trị, ta thực hiện các bước sau:

Tính đạo hàm y' = 3x^2 - 6x
Giải phương trình y' = 0 để tìm các điểm nghiệm: 3x^2 - 6x = 0 => x = 0 hoặc x = 2
Lập bảng biến thiên để xác định cực đại, cực tiểu.

Hy vọng với những hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải quyết Câu 20 trang 114 SGK Đại số và Giải tích 11 Nâng cao và các bài tập tương tự.