Câu 11 trang 80 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 11 Trang 80 SGK Hình Học 11 Nâng Cao
Bài tập Câu 11 trang 80 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng vào hình học không gian.
Dưới đây là lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và phương pháp giải bài tập này.
Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:
Đề bài
Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:
A. \({{{m^2}\sqrt 3 } \over 4}\)
B. \({{{{\left( {a - m} \right)}^2}\sqrt 2 } \over 2}\)
C. \({{{{\left( {a + m} \right)}^2}} \over 4}\)
D. \({{{{\left( {a - m} \right)}^2}\sqrt 3 } \over 4}\)
Lời giải chi tiết
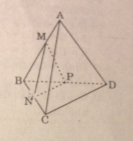
Vẽ MN // AC (N ϵ BC)
MP // AD (P ϵ BD)
Thiết diện cần tìm là ΔMNP
Ta có: \(\Delta MNP\backsim \Delta ACD\) tỉ số \({{MP} \over {AD}} = {{BM} \over {AB}} = {{a - m} \over a}\)
\( \Rightarrow \frac{{{S_{MNP}}}}{{{S_{ACD}}}} = {\left( {\frac{{MP}}{{AD}}} \right)^2} = {\left( {\frac{{a - m}}{a}} \right)^2}\)
\( \Rightarrow {S_{MNP}} = {\left( {{{a - m} \over a}} \right)^2}.{S_{ABC}} \)
\(= {\left( {{{a - m} \over a}} \right)^2}.{{{a^2}\sqrt 3 } \over 4} = {\left( {a - m} \right)^2}{{\sqrt 3 } \over 4}\)
Chọn (D)
Giải Chi Tiết Câu 11 Trang 80 SGK Hình Học 11 Nâng Cao
Câu 11 trang 80 SGK Hình học 11 Nâng cao yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học không gian. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
- Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng.
- Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
- Tích vô hướng của hai vectơ: a.b = |a||b|cos(θ)
- Ứng dụng của vectơ trong hình học: Chứng minh tính đồng phẳng, tính chất đường thẳng, mặt phẳng.
Phân tích bài toán Câu 11 Trang 80 SGK Hình Học 11 Nâng Cao
Trước khi đi vào giải chi tiết, chúng ta cần phân tích bài toán để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp các điểm trong không gian và yêu cầu chúng ta tính toán các vectơ, góc, hoặc chứng minh một mối quan hệ nào đó giữa các điểm và vectơ.
Lời Giải Chi Tiết Câu 11 Trang 80 SGK Hình Học 11 Nâng Cao
(Ở đây sẽ là lời giải chi tiết của câu 11 trang 80. Ví dụ, giả sử bài toán yêu cầu chứng minh ba điểm A, B, C thẳng hàng.)
Bước 1: Xác định các vectơ liên quan. Ví dụ: AB = B - A, AC = C - A
Bước 2: Kiểm tra xem hai vectơ có cùng phương hay không. Nếu AB = k.AC (với k là một số thực) thì ba điểm A, B, C thẳng hàng.
Bước 3: Kết luận.
Phương Pháp Giải Bài Toán Vectơ Trong Hình Học Không Gian
Để giải các bài toán vectơ trong hình học không gian một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
- Sử dụng tọa độ: Gán tọa độ cho các điểm và thực hiện các phép toán vectơ bằng tọa độ.
- Sử dụng tính chất của vectơ: Vận dụng các tính chất của vectơ để đơn giản hóa bài toán.
- Sử dụng tích vô hướng: Sử dụng tích vô hướng để tính góc giữa hai vectơ hoặc kiểm tra tính vuông góc.
- Sử dụng tích có hướng: Sử dụng tích có hướng để tìm vectơ pháp tuyến của một mặt phẳng.
Ví Dụ Minh Họa
Để hiểu rõ hơn về cách giải bài toán vectơ trong hình học không gian, chúng ta hãy xem xét một ví dụ sau:
(Ở đây sẽ là một ví dụ minh họa khác về bài toán vectơ)
Luyện Tập Thêm
Để củng cố kiến thức và kỹ năng giải bài toán vectơ, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Dưới đây là một số bài tập gợi ý:
- Bài tập 1: ...
- Bài tập 2: ...
- Bài tập 3: ...
Tổng Kết
Câu 11 trang 80 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán hình học không gian. Bằng cách nắm vững các kiến thức cơ bản, phân tích bài toán một cách cẩn thận và áp dụng các phương pháp giải phù hợp, bạn có thể giải quyết bài toán này một cách hiệu quả.
Chúc các em học tốt môn Hình học!