Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Câu 11 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, tập xác định và tập giá trị để giải quyết.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :
LG a
\(y = -\sin x\)
Lời giải chi tiết:
Đồ thị của hàm số \(y = -\sin x\) là hình đối xứng qua trục hoành của đồ thị hàm số \(y = \sin x\)
LG b
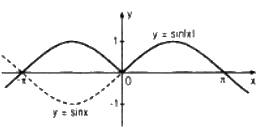
\(y = \left| {\sin x} \right|\)
Lời giải chi tiết:
Ta có: \(\left| {\sin x} \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,\sin x \ge 0} \cr { - \sin x\,\text{ nếu }\,\sin x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số \(y = |\sin x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách:
- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y ≥ 0\) (tức nửa mặt phẳng bên trên trục hoành kể cả bờ \(Ox\)).
- Lấy hình đối xứng qua trục hoành của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(y < 0\) (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ \(Ox\));
- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(y < 0\).
- Đồ thị \(y = |\sin x|\) là đường liền nét trong hình dưới đây :

LG c
\(y = \sin|x|\)
Lời giải chi tiết:
Ta có: \(\sin \left| x \right| = \left\{ {\matrix{{\sin x\,\text{ nếu }\,x \ge 0} \cr { - \sin x\,\text{ nếu }\,x < 0} \cr} } \right.\)
Do đó đồ thị của hàm số \(y = \sin|x|\) có được từ đồ thị \((C)\) của hàm số \(y = \sin x\) bằng cách :
- Giữ nguyên phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x ≥ 0\) (tức nửa mặt phẳng bên phải trục tung kể cả bờ \(Oy\)).
- Xóa phần đồ thị của \((C)\) nằm trong nửa mặt phẳng \(x < 0\) (tức nửa mặt phẳng bên trái trục tung không kể bờ \(Oy\)).
- Lấy hình đối xứng qua trục tung của phần đồ thị \((C)\) nằm trong nửa mặt phẳng \(x > 0\)
- Đồ thị \(y = \sin|x|\) là đường nét liền trong hình dưới đây :

Giải Chi Tiết Câu 11 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 11 trang 17 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I, tập trung vào việc ôn tập và củng cố kiến thức về hàm số. Bài tập này thường yêu cầu học sinh xác định tập xác định, tập giá trị, tính đơn điệu và các tính chất khác của hàm số. Việc nắm vững kiến thức nền tảng là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Nội Dung Bài Tập
Thông thường, câu 11 trang 17 sẽ đưa ra một hàm số cụ thể và yêu cầu học sinh thực hiện các thao tác sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Kiểm tra tính chẵn, lẻ của hàm số.
- Xét tính đơn điệu của hàm số (tăng, giảm).
- Vẽ đồ thị hàm số (nếu cần).
Phương Pháp Giải
Để giải quyết bài tập này, học sinh cần:
- Nắm vững định nghĩa và tính chất của hàm số: Hiểu rõ các khái niệm như tập xác định, tập giá trị, tính chẵn, lẻ, tính đơn điệu.
- Sử dụng các công thức và phương pháp đại số: Áp dụng các công thức biến đổi, giải phương trình, bất phương trình để tìm tập xác định, tập giá trị.
- Phân tích hàm số: Xác định các yếu tố quan trọng của hàm số như điểm cực trị, điểm uốn để xét tính đơn điệu.
- Vẽ đồ thị hàm số: Sử dụng các điểm đặc biệt và tính chất của hàm số để vẽ đồ thị một cách chính xác.
Ví Dụ Minh Họa
Giả sử hàm số được cho là: f(x) = √(2x - 1)
Bước 1: Xác định tập xác định:
Để hàm số có nghĩa, điều kiện là: 2x - 1 ≥ 0 => x ≥ 1/2. Vậy tập xác định của hàm số là D = [1/2, +∞).
Bước 2: Tìm tập giá trị:
Vì √(2x - 1) ≥ 0 với mọi x ≥ 1/2, nên tập giá trị của hàm số là [0, +∞).
Bước 3: Xét tính đơn điệu:
Đạo hàm của hàm số là: f'(x) = 1/√(2x - 1). Vì f'(x) > 0 với mọi x > 1/2, nên hàm số đồng biến trên khoảng (1/2, +∞).
Lưu Ý Quan Trọng
- Luôn kiểm tra điều kiện xác định của hàm số trước khi thực hiện bất kỳ phép toán nào.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.
- Luyện tập thường xuyên với nhiều bài tập khác nhau để nắm vững kiến thức và kỹ năng.
Tusach.vn - Nguồn Tài Liệu Học Tập Tin Cậy
Tusach.vn là một trang web cung cấp tài liệu học tập trực tuyến uy tín, với đội ngũ giáo viên giàu kinh nghiệm và nội dung được cập nhật thường xuyên. Chúng tôi cam kết mang đến cho học sinh những lời giải chi tiết, dễ hiểu và phương pháp học tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác và nâng cao kết quả học tập của bạn!
Chúc các em học tốt!