Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Câu 6 Trang 15 SGK Đại Số và Giải Tích 11 Nâng Cao
Bài tập Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Hãy cùng Tusach.vn khám phá cách giải bài tập này một cách hiệu quả nhất!
Cho hàm số y = f(x) = 2sin2x
LG a
Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
Ta có \(f(x + kπ) = 2\sin 2(x + kπ) \)
\(= 2\sin (2x + k2π) = 2\sin 2x = f(x),\) \( ∀ x \in\mathbb R\)
LG b
Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
Lời giải chi tiết:
Bảng biến thiên :
LG c
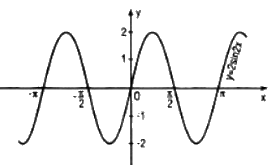
Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
Lời giải chi tiết:
Đồ thị :

Giải Chi Tiết Câu 6 Trang 15 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh các chủ đề về hàm số bậc hai, phương trình bậc hai, hoặc các bài toán liên quan đến đồ thị hàm số. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:
- Hàm số bậc hai: Định nghĩa, dạng tổng quát, tính chất (bề lõm, đỉnh, trục đối xứng).
- Phương trình bậc hai: Nghiệm, điều kiện có nghiệm, công thức nghiệm.
- Đồ thị hàm số bậc hai: Cách vẽ, các yếu tố quan trọng (đỉnh, trục đối xứng, giao điểm với trục tọa độ).
Phân Tích Đề Bài và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các thông tin đã cho và những gì cần tìm. Lập kế hoạch giải bài toán bằng cách chia nhỏ thành các bước nhỏ hơn. Ví dụ:
- Xác định hàm số bậc hai.
- Tìm điều kiện để phương trình có nghiệm.
- Giải phương trình bậc hai.
- Kết luận.
Ví Dụ Minh Họa (Giả sử đề bài là tìm m để phương trình x2 - 2(m+1)x + 2m + 3 = 0 có hai nghiệm phân biệt):
Bước 1: Xác định các hệ số a, b, c của phương trình bậc hai.
Trong phương trình x2 - 2(m+1)x + 2m + 3 = 0, ta có:
- a = 1
- b = -2(m+1)
- c = 2m + 3
Bước 2: Tính delta (Δ).
Δ = b2 - 4ac = [-2(m+1)]2 - 4(1)(2m + 3) = 4(m2 + 2m + 1) - 8m - 12 = 4m2 + 8m + 4 - 8m - 12 = 4m2 - 8
Bước 3: Điều kiện để phương trình có hai nghiệm phân biệt.
Phương trình có hai nghiệm phân biệt khi và chỉ khi Δ > 0.
4m2 - 8 > 0 ⇔ m2 > 2 ⇔ m > √2 hoặc m < -√2
Bước 4: Kết luận.
Vậy, để phương trình x2 - 2(m+1)x + 2m + 3 = 0 có hai nghiệm phân biệt thì m > √2 hoặc m < -√2.
Các Lưu Ý Quan Trọng
Khi giải các bài toán về hàm số bậc hai và phương trình bậc hai, cần lưu ý những điều sau:
- Kiểm tra kỹ các điều kiện của bài toán.
- Sử dụng đúng công thức và phương pháp giải.
- Biết cách trình bày lời giải một cách rõ ràng, logic.
- Thực hành giải nhiều bài tập khác nhau để nâng cao kỹ năng.
Tusach.vn – Nguồn Tài Liệu Học Tập Tin Cậy
Tusach.vn là một website cung cấp tài liệu học tập trực tuyến uy tín, với đội ngũ giáo viên giàu kinh nghiệm và nội dung được cập nhật thường xuyên. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Đại số và Giải tích 11 Nâng cao, giúp học sinh học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Chúc các em học tập tốt!