Giải Câu 11 Trang 106 SGK Đại số và Giải tích 11 Nâng cao

Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao

Giải Câu 11 Trang 106 SGK Đại số và Giải tích 11 Nâng cao

Bài tập Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Cho hình vuông

Đề bài

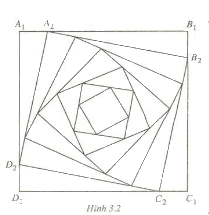
Cho hình vuông A₁B₁C₁D₁ có các cạnh bằng 6cm. Người ta dựng các hình vuông A₂B₂C₂D₂, A₃B₃C₃D₃, …, A_nB_nC_nD_n, … theo cách sau : Với mỗi n = 2, 3, 4, … lấy các điểm A_n, B_n , C_n, và D_n tương ứng trên các cạnh A_n-1B_n-1, B_n-1C_n-1, C_n-1D_n-1và D_n-1A_n-1 sao cho A_n-1A_n = 1cm và A_nB_nC_nD_n là một hình vuông (h.3.2). Xét dãy số (u_n) với u_n là độ dài cạnh của hình vuông A_nB_nC_nD_n.

Hãy cho dãy số (u_n) nói trên bởi hệ thức truy hồi.

Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao 1

Lời giải chi tiết

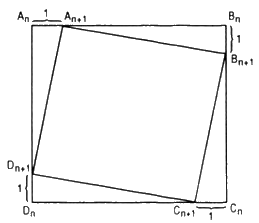
Với mỗi \(n \in \mathbb N^*\), xét các hình vuông \({A_n}{B_n}{C_n}{D_n}\) và \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}{D_{n + 1}},\) ta có

\(\eqalign{& {u_{n + 1}} = {A_{n + 1}}{B_{n + 1}} \cr&= \sqrt {{{\left( {{A_{n + 1}}{B_n}} \right)}^2} +{{\left( {{B_n}{B_{n + 1}}} \right)}^2}} \cr & = \sqrt {{{\left( {{A_n}{B_n} - 1} \right)}^2} + {1^2}} \cr & = \sqrt {{{\left( {{u_n} - 1} \right)}^2} + 1} \cr} \)

Giải Chi Tiết Câu 11 Trang 106 SGK Đại số và Giải tích 11 Nâng cao

Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao yêu cầu chúng ta xét hàm số f(x) = x³ - 3x² + 2 và tìm các điểm cực trị của hàm số này. Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:

Tìm tập xác định của hàm số: Hàm số f(x) = x³ - 3x² + 2 là một hàm đa thức, do đó tập xác định của hàm số là R (tập hợp tất cả các số thực).
Tính đạo hàm bậc nhất f'(x): f'(x) = 3x² - 6x
Tìm các điểm làm đạo hàm bậc nhất bằng 0: Giải phương trình f'(x) = 0, ta được: 3x² - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
Xác định dấu của đạo hàm bậc nhất trên các khoảng xác định:
- Khoảng (-∞; 0): Chọn x = -1, f'(-1) = 3(-1)² - 6(-1) = 9 > 0 => Hàm số đồng biến trên khoảng (-∞; 0)
- Khoảng (0; 2): Chọn x = 1, f'(1) = 3(1)² - 6(1) = -3 < 0 => Hàm số nghịch biến trên khoảng (0; 2)
- Khoảng (2; +∞): Chọn x = 3, f'(3) = 3(3)² - 6(3) = 9 > 0 => Hàm số đồng biến trên khoảng (2; +∞)
Kết luận về điểm cực trị:
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, do đó hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 0³ - 3(0)² + 2 = 2
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = 2³ - 3(2)² + 2 = 0

Vậy hàm số f(x) = x³ - 3x² + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là 0.

Lưu Ý Quan Trọng

Khi giải các bài toán về cực trị hàm số, điều quan trọng là phải xác định đúng dấu của đạo hàm bậc nhất trên các khoảng xác định. Việc này giúp chúng ta kết luận chính xác về điểm cực đại và cực tiểu của hàm số.

Bài Tập Tương Tự

Để củng cố kiến thức về cực trị hàm số, các em có thể tham khảo các bài tập tương tự sau:

Tìm cực trị của hàm số y = x⁴ - 4x² + 3
Tìm cực trị của hàm số y = -x³ + 3x² - 2

Tusach.vn - Nguồn Tài Liệu Học Tập Uy Tín

Tusach.vn là một website cung cấp tài liệu học tập trực tuyến uy tín, với đội ngũ giáo viên giàu kinh nghiệm và nội dung được cập nhật thường xuyên. Chúng tôi hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao và đạt kết quả tốt trong học tập.

Điểm	Giá trị
Cực đại	(0, 2)
Cực tiểu	(2, 0)

Câu 11 trang 106 SGK Đại số và Giải tích 11 Nâng cao