Câu 34 trang 118 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 34 Trang 118 SGK Hình Học 11 Nâng Cao
Câu 34 trang 118 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học Hình học không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng, quan hệ song song và quan hệ vuông góc để giải quyết.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho hình chóp S.ABCD có đáy là hình chữ nhật và Ab = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng
Đề bài
Cho hình chóp S.ABCD có đáy là hình chữ nhật và AB = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng \(a\sqrt 2 \)
a. Tính khoảng cách từ S đến mặt phẳng đáy (ABCD).
b. Gọi E và F lần lượt là trung điểm các cạnh AB và CD ; K là điểm bất kì thuộc đường thẳng AD. Chứng minh rằng khoảng cách giữa hai đường thẳng EF và SK không phụ thuộc vào K, hãy tính khoảng cách đó theo a.
Lời giải chi tiết
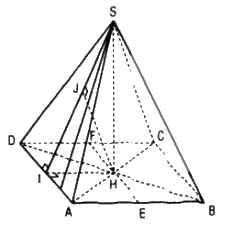
a. Gọi H là hình chiếu của S lên (ABCD).
Khi đó \(SH \bot \left( {ABCD} \right)\).
Xét các tam giác SHA, SHB, SHC, SHD có:
\(\widehat {SHA} = \widehat {SHB} = \widehat {SHC} = \widehat {SHD} = {90^0}\) (vì \(SH \bot \left( {ABCD} \right)\)
Chung SH
Nên \(\Delta SHA = \Delta SHB = \Delta SHC = \Delta SHD\) (2 cạnh góc vuông)
\( \Rightarrow HA = HB = HC = HD\)
\( \Rightarrow H\) là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
\( \Rightarrow H\) là giao điểm của AC và BD.
Ta có:
\(\eqalign{ & S{H^2} = S{A^2} - A{H^2} \cr&= S{A^2} - {\left( {\frac{{AC}}{2}} \right)^2}= S{A^2} - {{A{C^2}} \over 4} \cr&= 2{a^2} - {{A{B^2} + B{C^2}} \over 4} \cr & = 2{a^2} - {{4{a^2} + {a^2}} \over 4} = {{3{a^2}} \over 4}\cr&\Rightarrow SH = {{a\sqrt 3 } \over 2} \cr} \)
Cách khác:

b. Vì EF // AD nên EF // mp(SAD), mặt khác SK nằm trong mp(SAD) nên khoảng cách giữa EF và SK chính là khoảng cách giữa EF và mp(SAD), đó cũng chính là khoảng cách từ H đến mp(SAD).
Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD.
Tính d(EF ; SK) :
Gọi I là trung điểm của AD
\( \Rightarrow HI \bot AD\)
Mà \(AD \bot SH\) (do \(SH \bot \left( {ABCD} \right)\)
Nên \(AD \bot \left( {SHI} \right)\).
Kẻ đường cao HJ của tam giác vuông SHI thì
\(\left\{ \begin{array}{l}HJ \bot SI\\HJ \bot AD\left( {AD \bot \left( {SHI} \right)} \right)\end{array} \right.\)\( \Rightarrow HJ \bot \left( {SAD} \right)\)
Do đó d(H; (SAD)) = HJ.
Ta có: HJ.SI = SH.HI
\(S{I^2} = S{A^2} - A{I^2} = 2{a^2} - {{{a^2}} \over 4} = {{7{a^2}} \over 4}\)
Từ đó \(HJ = {{SH.HI} \over {SI}} = {{{{a\sqrt 3 } \over 2}.a} \over {{{a\sqrt 7 } \over 2}}} = {{a\sqrt {21} } \over 7}\)
Như vậy, khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD và bằng \({{a\sqrt {21} } \over 7}\)
Giải Chi Tiết Câu 34 Trang 118 SGK Hình Học 11 Nâng Cao
Câu 34 trang 118 SGK Hình học 11 Nâng cao thường xoay quanh việc xác định mối quan hệ giữa đường thẳng và mặt phẳng, hoặc giữa hai mặt phẳng. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Đường thẳng song song với mặt phẳng: Một đường thẳng song song với mặt phẳng nếu nó không có điểm chung với mặt phẳng đó.
- Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng nếu nó tạo với mặt phẳng một góc vuông.
- Hai mặt phẳng song song: Hai mặt phẳng song song nếu chúng không có điểm chung.
- Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc nếu góc giữa chúng bằng 90 độ.
Phân Tích Đề Bài (Ví dụ minh họa - đề bài cụ thể cần được thay thế):
Giả sử đề bài yêu cầu: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).
Để chứng minh điều này, ta cần:
- Chứng minh SM vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (ABCD).
- Thường thì hai đường thẳng này là AD và BC, hoặc AC và BD.
Lời Giải Chi Tiết (Ví dụ minh họa - cần điều chỉnh theo đề bài cụ thể):
Chứng minh:
Vì ABCD là hình vuông, M là trung điểm của CD nên AM ⊥ CD. Mặt khác, SA ⊥ (ABCD) nên SA ⊥ CD. Do đó, CD ⊥ (SAM). Suy ra CD ⊥ SM.
Tương tự, BM ⊥ CD và SA ⊥ CD, suy ra CD ⊥ (SBM). Do đó, CD ⊥ SM.
Vì SM ⊥ CD và SM ⊥ AD (do AD ⊥ (ABCD) và SM ⊥ (ABCD)), nên SM ⊥ (ABCD).
Các Dạng Bài Tập Liên Quan:
Ngoài dạng bài chứng minh quan hệ vuông góc, câu 34 trang 118 SGK Hình học 11 Nâng cao còn có thể xuất hiện các dạng bài tập sau:
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến một mặt phẳng.
- Xác định giao tuyến của hai mặt phẳng.
Mẹo Giải Bài Tập:
Để giải tốt các bài tập về đường thẳng và mặt phẳng, bạn nên:
- Vẽ hình chính xác và rõ ràng.
- Nắm vững các định lý và tính chất liên quan.
- Sử dụng phương pháp chứng minh gián tiếp.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Bảng Tổng Hợp Các Kiến Thức Quan Trọng:
| Khái niệm | Định nghĩa |
|---|---|
| Đường thẳng song song với mặt phẳng | Không có điểm chung |
| Đường thẳng vuông góc với mặt phẳng | Tạo góc 90 độ |
| Hai mặt phẳng song song | Không có điểm chung |
| Hai mặt phẳng vuông góc | Góc giữa chúng bằng 90 độ |
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải Câu 34 trang 118 SGK Hình học 11 Nâng cao. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác!