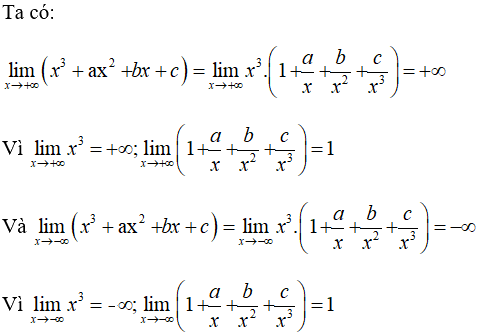Giải Câu 20 Trang 226 SGK Đại số và Giải tích 11 Nâng cao

Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng cao

Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về hàm số, đạo hàm, hoặc các chủ đề khác đã được học để giải quyết một vấn đề cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Chứng minh rằng phương trình

Đề bài

Chứng minh rằng phương trình \({x^3} + a{x^2} + bx + c = 0\) luôn có ít nhất một nghiệm.

Lời giải chi tiết

Đặt \(f(x)={x^3} + a{x^2} + bx + c = 0\)

Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng cao 1

Do \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \) nên có số \(α < 0\) sao cho \(f(α) < 0\).

Do \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên có số \(β > 0\) sao cho \(f(β) > 0\).

Hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) liên tục trên \(\mathbb R\) chứa đoạn \(\left[ {\alpha ;\beta } \right]\) nên theo định lý về giá trị trung gian của hàm số liên tục, tồn tại số \(d \in \left[ {\alpha ;\beta } \right]\) sao cho \(f(d) = 0\). Đó chính là nghiệm của phương trình \(f(x) = 0\).

Giải Chi Tiết Câu 20 Trang 226 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng cao thường thuộc các dạng bài tập về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến giới hạn. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản và kỹ năng giải toán.

Phân Tích Đề Bài và Xác Định Yêu Cầu

Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài, hiểu rõ yêu cầu và xác định các thông tin đã cho. Điều này giúp học sinh tránh được những sai sót không đáng có và tìm ra hướng giải quyết phù hợp.

Các Bước Giải Bài Tập (Ví dụ minh họa - cần thay thế bằng nội dung cụ thể của câu 20):

Bước 1: Xác định hàm số cần khảo sát. Ví dụ: y = f(x) = x³ - 3x² + 2
Bước 2: Tính đạo hàm bậc nhất y' = f'(x). Ví dụ: y' = 3x² - 6x
Bước 3: Tìm các điểm cực trị bằng cách giải phương trình y' = 0. Ví dụ: 3x² - 6x = 0 => x = 0 hoặc x = 2
Bước 4: Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.
Bước 5: Kết luận về tính chất của hàm số.

Lưu Ý Quan Trọng Khi Giải Bài Tập

Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Sử dụng công cụ hỗ trợ: Các công cụ tính toán trực tuyến hoặc phần mềm toán học có thể giúp học sinh giải bài tập nhanh chóng và chính xác hơn.
Luyện tập thường xuyên: Luyện tập thường xuyên là cách tốt nhất để nắm vững kiến thức và kỹ năng giải bài tập.

Ví Dụ Giải Chi Tiết (Thay thế bằng lời giải cụ thể của câu 20):

Đề bài: (Giả sử đây là đề bài của câu 20) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x³ - 3x² + 2 trên đoạn [-1; 3].

Lời giải:

Tính đạo hàm: y' = 3x² - 6x
Giải phương trình y' = 0: 3x² - 6x = 0 => x = 0 hoặc x = 2
Tính giá trị của hàm số tại các điểm cực trị và các đầu mút của đoạn:

y(-1) = (-1)³ - 3(-1)² + 2 = -2
y(0) = 0³ - 3(0)² + 2 = 2
y(2) = 2³ - 3(2)² + 2 = -2
y(3) = 3³ - 3(3)² + 2 = 2

So sánh các giá trị, ta có:

Giá trị lớn nhất của hàm số trên đoạn [-1; 3] là 2.
Giá trị nhỏ nhất của hàm số trên đoạn [-1; 3] là -2.

Tổng Kết

Việc giải Câu 20 trang 226 SGK Đại số và Giải tích 11 Nâng cao đòi hỏi sự hiểu biết vững chắc về các khái niệm và kỹ năng toán học. tusach.vn hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải bài tập.

Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ!