Giải Câu 12 Trang 195 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao

Giải Câu 12 Trang 195 SGK Đại số và Giải tích 11 Nâng cao

Bài tập Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Hình 5.4 là đồ thị của hàm số y = f(x) trên

Đề bài

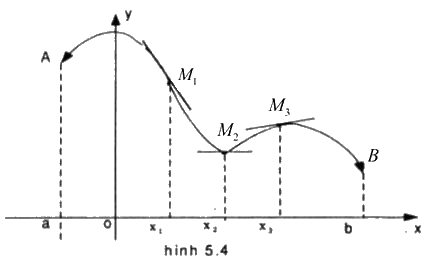
Hình 5.4 là đồ thị của hàm số y = f(x) trên khoảng (a ; b). Biết rằng tại các điểm M₁, M₂ và M₃, đồ thị hàm số có tiếp tuyến được thể hiện trên hình vẽ. Dựa vào hình vẽ, em hãy nêu nhận xét về dấu của \(f'\left( {{x_1}} \right),f'\left( {{x_2}} \right)\,va\,f'\left( {{x_3}} \right)\)

Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao 1

Lời giải chi tiết

Đồ thị của hàm số y = f(x) có tiếp tuyến tại các điểm M₁, M₂ và M₃ nên hàm số y = f(x) có đạo hàm tại các điểm x₁, x₂ và x₃. Ta nhận thấy :

+ Tiếp tuyến tại các điểm M₁ là một đường thẳng “đi xuống” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số âm, suy ra \(f'\left( {{x_1}} \right) < 0\)

+ Tiếp tuyến tại điểm M₂ là một đường thẳng song song với trục hoành nên hệ số góc của tiếp tuyến bằng 0, suy ra \(f'\left( {{x_2}} \right) = 0\)

+ Tiếp tuyến tại điểm M₃ là một đường thẳng “đi lên” từ trái sang phải, nên hệ số góc của tiếp tuyến là một số dương, suy ra \(f'\left( {{x_3}} \right) > 0\)

Giải Chi Tiết Câu 12 Trang 195 SGK Đại số và Giải tích 11 Nâng cao

Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học kỳ I lớp 11, tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.

Đề Bài Câu 12 Trang 195 SGK Đại số và Giải tích 11 Nâng cao

(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hàm số y = x³ - 3x² + 2. Hãy tìm các điểm cực trị của hàm số.)

Phương Pháp Giải

Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Tính đạo hàm cấp một (y'): Đạo hàm cấp một của hàm số cho biết độ dốc của tiếp tuyến tại mỗi điểm trên đồ thị hàm số.
Tìm các điểm cực trị: Giải phương trình y' = 0 để tìm các giá trị của x mà tại đó đạo hàm bằng không. Các giá trị này là các điểm nghi ngờ là cực trị.
Xác định loại cực trị: Sử dụng đạo hàm cấp hai (y'') hoặc xét dấu của đạo hàm cấp một để xác định xem các điểm nghi ngờ là cực đại hay cực tiểu.
Tính giá trị của hàm số tại các điểm cực trị: Thay các giá trị x của điểm cực trị vào hàm số ban đầu để tìm giá trị y tương ứng.
Kết luận: Nêu rõ các điểm cực đại, cực tiểu và giá trị tương ứng.

Lời Giải Chi Tiết

(Lời giải chi tiết cho đề bài cụ thể sẽ được chèn vào đây. Bao gồm các bước tính toán, giải thích rõ ràng và kết luận.)

Ví Dụ Minh Họa

Để hiểu rõ hơn về phương pháp giải, chúng ta hãy xem xét một ví dụ khác:

(Ví dụ minh họa với một hàm số tương tự và lời giải chi tiết.)

Lưu Ý Quan Trọng

Luôn kiểm tra điều kiện xác định của hàm số trước khi thực hiện các phép toán đạo hàm.
Sử dụng đạo hàm cấp hai một cách cẩn thận để xác định chính xác loại cực trị.
Vẽ đồ thị hàm số sau khi tìm được các điểm cực trị để kiểm tra lại kết quả.

Bài Tập Tương Tự

Để rèn luyện kỹ năng giải bài tập, bạn có thể thử giải các bài tập tương tự sau:

Bài tập 1: (Đề bài)
Bài tập 2: (Đề bài)
Bài tập 3: (Đề bài)

Tổng Kết

Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững phương pháp giải và thực hành thường xuyên sẽ giúp học sinh tự tin hơn khi giải các bài tập tương tự.

tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các bạn học sinh sẽ hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.

Câu 12 trang 195 SGK Đại số và Giải tích 11 Nâng cao