Giải Câu 1 Trang 124 SGK Hình học 11 Nâng cao

Câu 1 trang 124 SGK Hình học 11 Nâng cao

Giải Câu 1 Trang 124 SGK Hình học 11 Nâng cao

Bài tập Câu 1 trang 124 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian.

Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng vào giải quyết các bài toán thực tế.

tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.

Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

Đề bài

Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

a. Xét bốn tam giác APN, PBM, NMC, MNP. Tìm phép dời hình biến tam giác APN lần lượt thành một trong ba tam giác còn lại.

b. Phép vị tự nào biến tam giác ABC thành tam giác MNP ?

c. Xét tam giác có ba đỉnh là trực tâm của ba tam giác APN, PBM và NCM. Chứng tỏ rằng tam giác đó bằng tam giác APN. Chứng minh điều đó cũng đúng nếu thay trực tâm bằng trọng tâm, hoặc tâm đường tròn ngoại tiếp hoặc tâm đường tròn nội tiếp.

Lời giải chi tiết

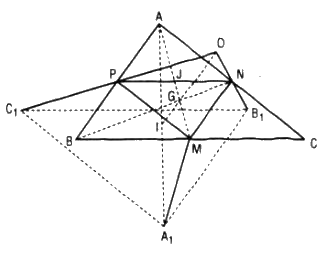
Câu 1 trang 124 SGK Hình học 11 Nâng cao 1

a. Phép tịnh tiến \({T_{\overrightarrow {AP} }}\) biến tam giác APN thành tam giác PBM.

Phép tịnh tiến \({T_{\overrightarrow {AN} }}\) biến tam giác APN thành tam giác NMC. Phép đối xứng tâm Đ_J, với J là trung điểm của PN, biến tam giác APN thành tam giác MNP.

b. Gọi G là trọng tâm của tam giác ABC thì \(\overrightarrow {GM} = - {1 \over 2}\overrightarrow {GA} ,\overrightarrow {GN} = - {1 \over 2}\overrightarrow {GB} ,\overrightarrow {GP} = - {1 \over 2}\overrightarrow {GC} .\)

Vậy phép vị tự tâm G, tỉ số \(k = - {1 \over 2}\) biến tam giác ABC thành tam giác MNP.

c. Gọi H₁, H₂, H₃ lần lượt là trực tâm của tam giác APN, PBM, NMC.

Phép tịnh tiến \({T_{\overrightarrow {AP} }}\) biến APN thành tam giác PBM nên biến H₁ thành H₂, tức là \(\overrightarrow {{H_1}{H_2}} = \overrightarrow {AP} \,hay\,\overrightarrow {A{H_1}} = \overrightarrow {P{H_2}} .\) Tương tự ta có \(\overrightarrow {{H_1}{H_3}} = \overrightarrow {AN} \,hay\,\overrightarrow {A{H_1}} = \overrightarrow {N{H_3}} .\)

Vậy \(\overrightarrow {A{H_1}} = \overrightarrow {P{H_2}} = \overrightarrow {N{H_3}} .\) Từ đó suy ra phép tịnh tiến theo vecto \(\overrightarrow {A{H_1}} \) biến tam giác APN thành tam giác H₁H₂H₃.

Đối với các trường hợp khác (trọng tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp), chứng minh hoàn toàn tương tự.

Giải Chi Tiết Câu 1 Trang 124 SGK Hình học 11 Nâng cao

Câu 1 trang 124 SGK Hình học 11 Nâng cao thuộc chương trình học về vectơ trong không gian. Bài toán này thường yêu cầu học sinh chứng minh một đẳng thức vectơ hoặc tìm một vectơ thỏa mãn điều kiện cho trước. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:

Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng.
Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
Các tính chất của phép toán vectơ: Tính giao hoán, tính kết hợp, tính chất phân phối.
Ứng dụng của vectơ: Biểu diễn các điểm, đường thẳng, mặt phẳng trong không gian.

Phân Tích Bài Toán

Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Sau đó, chúng ta cần phân tích bài toán để tìm ra hướng giải quyết phù hợp. Thông thường, chúng ta có thể sử dụng các phương pháp sau để giải bài toán vectơ:

Phương pháp hình học: Sử dụng các tính chất hình học để chứng minh đẳng thức vectơ.
Phương pháp tọa độ: Sử dụng hệ tọa độ để biểu diễn các vectơ và thực hiện các phép toán vectơ.
Phương pháp vectơ: Sử dụng các định lý và tính chất của vectơ để giải bài toán.

Lời Giải Chi Tiết

(Giả sử đề bài Câu 1 trang 124 SGK Hình học 11 Nâng cao là: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: overrightarrow{AB} +overrightarrow{AD} +overrightarrow{AA'} =overrightarrow{AC'})

Lời giải:

Ta có: overrightarrow{AC'} =overrightarrow{AB} +overrightarrow{BC'} =overrightarrow{AB} +overrightarrow{AD} +overrightarrow{DD'} +overrightarrow{D'C'}

Mà overrightarrow{DD'} =overrightarrow{AA'}

Và overrightarrow{D'C'} =overrightarrow{DC}

Suy ra: overrightarrow{AC'} =overrightarrow{AB} +overrightarrow{AD} +overrightarrow{AA'} +overrightarrow{DC}

Do đó: overrightarrow{AB} +overrightarrow{AD} +overrightarrow{AA'} =overrightarrow{AC'} -overrightarrow{DC}

(Lưu ý: Đây chỉ là một ví dụ minh họa. Lời giải cụ thể sẽ phụ thuộc vào đề bài của Câu 1 trang 124 SGK Hình học 11 Nâng cao.)

Mở Rộng và Bài Tập Tương Tự

Để củng cố kiến thức về vectơ, các em có thể làm thêm các bài tập tương tự. Một số bài tập gợi ý:

Chứng minh đẳng thức vectơ khác.
Tìm vectơ thỏa mãn điều kiện cho trước.
Ứng dụng vectơ để giải các bài toán hình học không gian.

Kết Luận

Câu 1 trang 124 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp các em học sinh hiểu sâu hơn về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các gợi ý trên, các em sẽ tự tin giải quyết bài toán này và các bài toán tương tự một cách hiệu quả.

Chúc các em học tốt!

Khái niệm	Giải thích
Vectơ	Một đoạn thẳng có hướng.
Phép cộng vectơ	Quy tắc hình bình hành.
Phép nhân vectơ với một số thực	Thay đổi độ dài của vectơ.
Nguồn: tusach.vn

Câu 1 trang 124 SGK Hình học 11 Nâng cao