Câu 2 trang 120 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 2 Trang 120 SGK Hình Học 11 Nâng Cao
Câu 2 trang 120 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.
Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
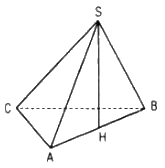
Cho hình chóp S.ABC có SA = Sb = SC = a,
Đề bài
Cho hình chóp S.ABC có SA = SB = SC = a, \(\widehat {ASB} = 120^\circ ,\widehat {BSC} = 60^\circ ,\widehat {CSA} = 90^\circ \) .
a. Chứng tỏ rằng ABC là tam giác vuông
b. Tính khoảng cách từ S đến mặt phẳng (ABC)
Lời giải chi tiết
a. Ta có:
\(\eqalign{ & \overrightarrow {CA} .\overrightarrow {CB} \cr &= \left( {\overrightarrow {SA} - \overrightarrow {SC} } \right)\left( {\overrightarrow {SB} - \overrightarrow {SC} } \right) \cr & = \overrightarrow {SA} .\overrightarrow {SB} - \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SC} .\overrightarrow {SB} + S{C^2} \cr & = {a^2}\cos 120^\circ - {a^2}\cos 90^\circ - {a^2}\cos 60^\circ + {a^2} \cr & = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \cr & \Rightarrow CA \bot CB \cr} \)
⇒ ΔABC vuông tại C.
b. Kẻ SH ⊥ mp(ABC), do SA = SB = SC nên HA = HB = HC mà ΔABC vuông tại C nên H là trung điểm của AB.
Áp dụng định lí cô sin vào tam giác ABC, ta có:
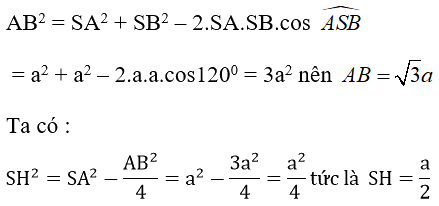
Giải Chi Tiết Câu 2 Trang 120 SGK Hình Học 11 Nâng Cao
Câu 2 trang 120 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, các phép toán vectơ, điều kiện đồng phẳng của ba vectơ, và phương trình mặt phẳng.
Đề Bài Câu 2 Trang 120 SGK Hình Học 11 Nâng Cao
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho bốn điểm A, B, C, D không đồng phẳng. Chứng minh rằng bốn điểm đó tạo thành một tứ diện.)
Lời Giải Chi Tiết
Để chứng minh bốn điểm A, B, C, D tạo thành một tứ diện, ta cần chứng minh rằng bốn điểm này không đồng phẳng. Điều này có nghĩa là ba vectơ AB, AC, AD không đồng phẳng.
Để chứng minh ba vectơ không đồng phẳng, ta có thể tính tích hỗn hợp của chúng. Nếu tích hỗn hợp khác 0, thì ba vectơ đó không đồng phẳng.
Tích hỗn hợp của ba vectơ AB, AC, AD được tính như sau:
[AB, AC, AD] = (AB x AC) . AD
Trong đó:
- AB x AC là tích vector của AB và AC.
- (AB x AC) . AD là tích vô hướng của tích vector (AB x AC) và AD.
Nếu kết quả tính toán tích hỗn hợp khác 0, thì bốn điểm A, B, C, D không đồng phẳng và do đó tạo thành một tứ diện.
Ví Dụ Minh Họa
Giả sử A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6). Ta tính:
AB = (1; 1; 1)
AC = (2; 2; 2)
AD = (3; 3; 3)
Ta thấy AC = 2AB và AD = 3AB. Điều này có nghĩa là ba vectơ AB, AC, AD cùng phương, do đó chúng đồng phẳng. Vậy bốn điểm A, B, C, D đồng phẳng và không tạo thành một tứ diện.
Lưu Ý Quan Trọng
Khi giải các bài toán liên quan đến đường thẳng và mặt phẳng, học sinh cần chú ý:
- Nắm vững định nghĩa và tính chất của vectơ.
- Thành thạo các phép toán vectơ (cộng, trừ, nhân với một số, tích vô hướng, tích vector).
- Hiểu rõ điều kiện đồng phẳng của ba vectơ.
- Biết cách viết phương trình mặt phẳng.
Tusach.vn - Đồng Hành Cùng Bạn Học Toán
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các bài tập luyện tập để giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!