Câu 29 trang 117 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 29 Trang 117 SGK Hình Học 11 Nâng Cao
Câu 29 trang 117 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng, đặc biệt là các tính chất về quan hệ song song, vuông góc.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và phương pháp giải bài tập này.
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Đề bài
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Lời giải chi tiết
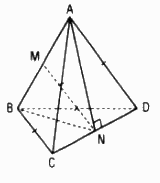
Gọi M, N lần lượt là trung điểm của AB và CD
ΔACD cân nên AN ⊥ CD và ΔBCD cân nên BN ⊥ CD.
Do đó CD ⊥ (ABN) suy ra CD ⊥ MN.
Tương tự ta cũng có AB ⊥ MN
Vậy d(AB, CD) = MN
Ta có:
\(\eqalign{ & M{N^2} = A{N^2} - A{M^2} = A{D^2} - N{D^2} - A{M^2} \cr & = {a^2} - {{c{'^2}} \over 4} - {{{c^2}} \over 4} = {1 \over 4}\left( {4{a^2} - c{'^2} - {c^2}} \right) \cr} \)
Vậy \(MN = {1 \over 2}\sqrt {4{a^2} - c{'^2} - {c^2}} \) với điều kiện \(4{a^2} > {c^2} + c{'^2}\)
Giải Chi Tiết Câu 29 Trang 117 SGK Hình Học 11 Nâng Cao
Câu 29 trang 117 SGK Hình học 11 Nâng cao thường xoay quanh việc xác định mối quan hệ giữa đường thẳng và mặt phẳng, hoặc giữa hai mặt phẳng. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Đường thẳng song song với mặt phẳng: Một đường thẳng song song với mặt phẳng nếu nó không có điểm chung với mặt phẳng đó.
- Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng nếu nó tạo với mặt phẳng một góc vuông.
- Hai mặt phẳng song song: Hai mặt phẳng song song nếu chúng không có điểm chung.
- Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc nếu góc giữa chúng bằng 90 độ.
Phân Tích Đề Bài (Ví dụ minh họa - đề bài cụ thể cần được thay thế):
Giả sử đề bài yêu cầu chứng minh một đường thẳng song song với một mặt phẳng. Bước đầu tiên là xác định các yếu tố liên quan: đường thẳng cần xét, mặt phẳng cần xét và các thông tin khác được cung cấp trong đề bài.
Phương Pháp Giải:
Để chứng minh một đường thẳng song song với một mặt phẳng, ta có thể sử dụng một trong các phương pháp sau:
- Phương pháp 1: Chứng minh đường thẳng đó song song với một đường thẳng nào đó nằm trong mặt phẳng.
- Phương pháp 2: Chứng minh đường thẳng đó không có điểm chung với mặt phẳng.
- Phương pháp 3: Sử dụng các định lý về quan hệ song song trong không gian.
Lời Giải Chi Tiết (Ví dụ minh họa - cần thay thế bằng lời giải cụ thể của câu 29):
(Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết. Ví dụ:
Gọi I là giao điểm của đường thẳng d với mặt phẳng (P). Ta chứng minh rằng I không tồn tại, tức là d song song với (P). Để chứng minh điều này, ta xét hệ phương trình giao điểm của d và (P). Nếu hệ phương trình vô nghiệm, thì d song song với (P).
...)
Lưu Ý Quan Trọng:
Khi giải các bài toán về quan hệ song song, vuông góc trong không gian, cần chú ý:
- Vẽ hình chính xác và rõ ràng.
- Sử dụng các định lý và tính chất một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải xong.
Bài Tập Tương Tự:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao. Tusach.vn sẽ tiếp tục cập nhật lời giải chi tiết cho các bài tập khác trong chương trình học.
Bảng Tóm Tắt Các Kiến Thức Liên Quan:
| Khái niệm | Định nghĩa |
|---|---|
| Đường thẳng song song với mặt phẳng | Không có điểm chung |
| Đường thẳng vuông góc với mặt phẳng | Tạo góc vuông |
| Hai mặt phẳng song song | Không có điểm chung |
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về Câu 29 trang 117 SGK Hình học 11 Nâng cao và có thể tự tin giải các bài tập tương tự. Chúc các em học tốt!