Câu 33 trang 212 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 33 Trang 212
Chào mừng các em học sinh đến với lời giải chi tiết của Câu 33 trang 212 SGK Đại số và Giải tích 11 Nâng cao. Bài tập này thuộc chương trình học kỳ I, tập trung vào kiến thức về hàm số và đồ thị hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các bài tập tương tự để các em luyện tập và củng cố kiến thức.
Tìm đạo hàm của mỗi hàm số sau :
LG a
\(\displaystyle y = {{\sin x} \over x} + {x \over {{\mathop{\rm sinx}\nolimits} }}\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = \dfrac{{\left( {\sin x} \right)'.x - \sin x.\left( {x'} \right)}}{{{x^2}}}\) \( + \dfrac{{x'\sin x - x.\left( {\sin x} \right)'}}{{{{\sin }^2}x}}\)
\(\eqalign{ & = {{x\cos x - \sin x} \over {{x^2}}} + {{\sin x - x\cos x} \over {{{\sin }^2}x}} \cr & = \left( {x\cos x - {\mathop{\rm sinx}\nolimits} } \right)\left( {{1 \over {{x^2}}} - {1 \over {{{\sin }^2}x}}} \right) \cr} \)
LG b
\(\displaystyle y = {{{{\sin }^2}x} \over {1 + \tan 2x}}\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
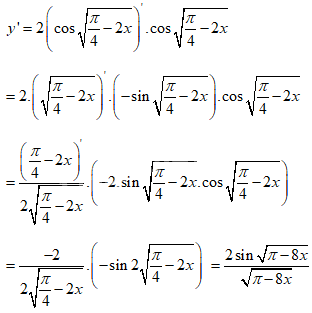
LG c
\(y = \tan \left( {\sin x} \right)\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = \left( {\sin x} \right)'.\dfrac{1}{{{{\cos }^2}\left( {\sin x} \right)}}\) \( \displaystyle = {{\cos x} \over {{{\cos }^2}\left( {\sin x} \right)}}\)
LG d
\(y = x\cot \left( {{x^2} - 1} \right)\)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = x'.\cot \left( {{x^2} - 1} \right) + x.\left[ {\cot \left( {{x^2} - 1} \right)} \right]'\) \( = \cot \left( {{x^2} - 1} \right) + x.\left( {{x^2} - 1} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}\left( {{x^2} - 1} \right)}}\)
\(\eqalign{ & = \cot \left( {{x^2} - 1} \right) + x.{{ - 2x} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr & = \cot \left( {{x^2} - 1} \right) - {{2{x^2}} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr} \)
LG e
\(\displaystyle y = {\cos ^2}\sqrt {{\pi \over 4} - 2x} \)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
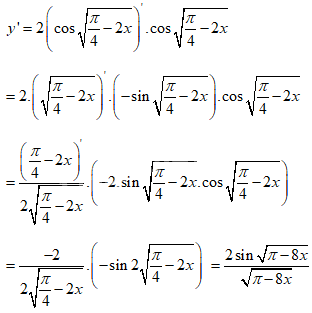
LG f
\(y = x\sqrt {\sin 3x} \)
Phương pháp giải:
Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp.
Giải chi tiết:
\(y' = x'\sqrt {\sin 3x} + x.\left( {\sqrt {\sin 3x} } \right)'\) \( = \sqrt {\sin 3x} + x.\dfrac{{\left( {\sin 3x} \right)'}}{{2\sqrt {\sin 3x} }}\) \( \displaystyle = \sqrt {\sin 3x} + x.{{3\cos 3x} \over {2\sqrt {\sin 3x} }} \) \(\displaystyle = {{2\sin 3x + 3x\cos 3x} \over {2\sqrt {\sin 3x} }}\)
Giải Chi Tiết Câu 33 Trang 212 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 33 trang 212 SGK Đại số và Giải tích 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về hàm số bậc hai, đặc biệt là việc xác định hệ số a, b, c và các yếu tố của parabol (đỉnh, trục đối xứng, giao điểm với trục hoành, trục tung) để giải quyết bài toán.
Nội Dung Bài Tập
Thông thường, dạng bài tập này sẽ yêu cầu:
- Xác định parabol đi qua các điểm cho trước.
- Tìm tọa độ đỉnh của parabol.
- Tìm trục đối xứng của parabol.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Vẽ đồ thị hàm số.
Phương Pháp Giải
Để giải quyết bài tập này, chúng ta cần thực hiện các bước sau:
- Bước 1: Xác định dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c.
- Bước 2: Thay tọa độ các điểm mà parabol đi qua vào phương trình hàm số để tạo thành hệ phương trình.
- Bước 3: Giải hệ phương trình để tìm các hệ số a, b, c.
- Bước 4: Sử dụng các công thức để tính toán các yếu tố của parabol:
- Hoành độ đỉnh: xđỉnh = -b / (2a)
- Tung độ đỉnh: yđỉnh = -Δ / (4a) (với Δ = b2 - 4ac)
- Trục đối xứng: x = -b / (2a)
- Bước 5: Xác định giao điểm của parabol với trục hoành (nghiệm của phương trình ax2 + bx + c = 0) và trục tung (x = 0).
- Bước 6: Dựa vào hệ số a để xác định chiều mở của parabol (a > 0: mở lên, a < 0: mở xuống).
- Bước 7: Vẽ đồ thị hàm số.
Ví Dụ Minh Họa
Giả sử đề bài yêu cầu tìm parabol y = ax2 + bx + c đi qua các điểm A(0; 1), B(1; 2), C(-1; 0). Ta sẽ thực hiện như sau:
Thay tọa độ các điểm vào phương trình:
- A(0; 1): 1 = a(0)2 + b(0) + c => c = 1
- B(1; 2): 2 = a(1)2 + b(1) + c => a + b + c = 2
- C(-1; 0): 0 = a(-1)2 + b(-1) + c => a - b + c = 0
Thay c = 1 vào hai phương trình còn lại, ta được:
- a + b = 1
- a - b = -1
Giải hệ phương trình này, ta được a = 0 và b = 1. Vậy phương trình parabol là y = x + 1.
Lưu Ý Quan Trọng
Khi giải bài tập về hàm số bậc hai, cần chú ý:
- Kiểm tra kỹ các điều kiện của bài toán.
- Sử dụng đúng các công thức và phương pháp giải.
- Vẽ đồ thị hàm số một cách chính xác.
Bài Tập Tương Tự
Để luyện tập thêm, các em có thể tham khảo các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Tusach.vn sẽ tiếp tục cập nhật thêm nhiều lời giải chi tiết và bài tập luyện tập để hỗ trợ các em học tập tốt hơn.
Chúc các em học tập tốt!