Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Câu 19 Trang 29 SGK Đại số và Giải tích 11 Nâng cao
Bài tập Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
a.Vẽ đồ thị của hàm số y = tanx rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng (-π ; π) là nghiệm của mỗi phương trình sau
LG a
Vẽ đồ thị của hàm số \(y = \tan x\) rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng \((-π ; π)\) là nghiệm của mỗi phương trình sau
1. \(\tan x = -1\)
2. \(\tan x = 0\)
Lời giải chi tiết:
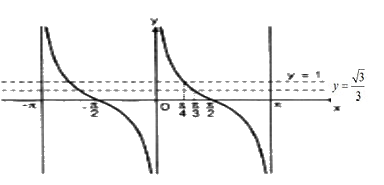
1. Phương trình \(\tan x = -1\) có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = - {\pi \over 4}\,\text{ và }\,x = {{3\pi } \over 4}\)
2. Phương trình \(\tan x = 0\) có nghiệm thuộc khoảng \((-π ; π)\) là \(x = 0\)
LG b
Cũng câu hỏi tương tự cho hàm số \(y = \cot x\) và cho mỗi phương trình sau
1. \(\cot x = {{\sqrt 3 } \over 3}\)
2. \(\cot x = 1\)
Lời giải chi tiết:

1. Phương trình có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = {\pi \over 3}\,\text{ và }\,x = - {{2\pi } \over 3}\)
2. Phương trình \(\cot x = 1\) có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = {\pi \over 4}\,\text{ và }\,x = - {{3\pi } \over 4}\)
Giải Chi Tiết Câu 19 Trang 29 SGK Đại số và Giải tích 11 Nâng cao
Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
- Đạo hàm: Khái niệm đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Tính đơn điệu của hàm số: Mối liên hệ giữa đạo hàm và tính đơn điệu. Hàm số đồng biến khi đạo hàm dương, nghịch biến khi đạo hàm âm.
- Điều kiện xác định của hàm số: Xác định tập xác định của hàm số để đảm bảo tính hợp lệ của các phép toán.
Phân tích đề bài và xác định hướng giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài, xác định hàm số cần xét và yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu xét tính đơn điệu của hàm số trên một khoảng xác định. Việc xác định đúng khoảng xét là rất quan trọng.
Các bước giải chi tiết
- Tính đạo hàm f'(x) của hàm số f(x). Sử dụng các quy tắc tính đạo hàm đã học.
- Xác định các điểm mà f'(x) = 0 hoặc f'(x) không xác định. Đây là các điểm tới hạn của hàm số.
- Lập bảng xét dấu f'(x). Chia khoảng xác định của hàm số thành các khoảng dựa trên các điểm tới hạn. Xác định dấu của f'(x) trên mỗi khoảng.
- Kết luận về tính đơn điệu của hàm số. Dựa vào bảng xét dấu f'(x), kết luận hàm số đồng biến trên các khoảng mà f'(x) > 0 và nghịch biến trên các khoảng mà f'(x) < 0.
Ví dụ minh họa (Giả sử đề bài là xét tính đơn điệu của hàm số f(x) = x3 - 3x2 + 2 trên R)
Bước 1: Tính đạo hàm
f'(x) = 3x2 - 6x
Bước 2: Xác định điểm tới hạn
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Bước 3: Lập bảng xét dấu
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 4: Kết luận
Hàm số f(x) = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Lưu ý quan trọng
- Luôn kiểm tra lại các bước tính toán để tránh sai sót.
- Chú ý đến tập xác định của hàm số.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.
Tusach.vn hy vọng với lời giải chi tiết này, các bạn học sinh sẽ hiểu rõ hơn về cách giải Câu 19 trang 29 SGK Đại số và Giải tích 11 Nâng cao. Chúc các bạn học tốt!