Giải Câu 10 Trang 13 SGK Hình Học 11 Nâng Cao

Câu 10 trang 13 SGK Hình học 11 Nâng cao

Giải Câu 10 Trang 13 SGK Hình Học 11 Nâng Cao

Bài tập Câu 10 trang 13 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ để giải quyết các bài toán liên quan đến hình học không gian.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hai điểm B,C cố định nằm trên đường tròn

Đề bài

Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định

Hướng dẫn : Khi BC không phải là đường kính, gọi H’ là giao điểm của đường thẳng AH với đường tròn (O; R). Chứng minh rằng H đối xứng với H’ qua đường thẳng BC.

Lời giải chi tiết

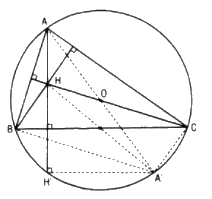
Trường hợp BC là đường kính thì tam giác ABC vuông tại A nên H trùng A

Do đó H nằm trên đường tròn cố định (O ; R)

Xét trường hợp BC không là đường kính.

Giả sử đường thẳng AH cắt đường tròn (O ; R) tại H’.

Gọi AA’ là đường kính của đường tròn (O ; R) thì:

A’B // CH (vì cùng vuông góc với AB)

A’C // BH (vì cùng vuông góc với AC)

Do đó A’BHC là hình bình hành.

Vậy BC đi qua trung điểm của HA’

Mặt khác BC // A’H’ (vì cùng vuông góc với AH) nên BC cũng đi qua trung điểm của HH’

(do BC đi qua trung điểm của HA' và song song A'H' nên đi qua trung điểm của HH')

Do đó H và H’ đối xứng với nhau qua BC.

Nếu gọi Đ là phép đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H.

Nhưng H’ luôn luôn nằm trên (O ; R) nên H nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ

Cách khác: Gọi H’ là điểm đối xứng của H qua BC. Chứng minh tứ giác ABH’C nội tiếp, từ đó suy ra H’ nằm trên (O ; R).

Giải Chi Tiết Câu 10 Trang 13 SGK Hình Học 11 Nâng Cao

Câu 10 trang 13 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh đẳng thức vectơ, xác định mối quan hệ giữa các vectơ, hoặc tính toán các đại lượng hình học liên quan đến vectơ. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:

Các phép toán vectơ: Cộng, trừ, nhân với một số thực, tích vô hướng, tích có hướng.
Các tính chất của vectơ: Tính giao hoán, tính kết hợp, tính chất phân phối.
Ứng dụng của vectơ trong hình học không gian: Biểu diễn các điểm, đường thẳng, mặt phẳng bằng vectơ.

Phân Tích Bài Toán và Lập Kế Hoạch Giải

Trước khi bắt tay vào giải bài toán, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, lập kế hoạch giải bài toán bằng cách:

Vẽ hình: Vẽ hình minh họa bài toán để dễ dàng hình dung và tìm ra mối liên hệ giữa các yếu tố.
Chọn hệ tọa độ: Chọn hệ tọa độ thích hợp để biểu diễn các điểm, vectơ bằng tọa độ.
Sử dụng các công thức: Áp dụng các công thức liên quan đến vectơ để tính toán và chứng minh.

Lời Giải Chi Tiết

(Giả sử đề bài Câu 10 trang 13 SGK Hình học 11 Nâng cao là: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của AB. Chứng minh rằng: vectơ AI = 1/2 vectơ AB)

Lời giải:

Vì I là trung điểm của AB, theo định nghĩa trung điểm ta có:

vectơ AI = 1/2 vectơ AB

Vậy, ta đã chứng minh được vectơ AI = 1/2 vectơ AB.

Các Dạng Bài Tập Tương Tự và Mở Rộng

Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự liên quan đến vectơ trong hình học không gian. Một số dạng bài tập thường gặp bao gồm:

Chứng minh đẳng thức vectơ.
Tìm mối quan hệ giữa các vectơ.
Tính độ dài của vectơ.
Tính góc giữa hai vectơ.
Ứng dụng vectơ để giải các bài toán về hình học phẳng và hình học không gian.

Lưu Ý Khi Giải Bài Tập Vectơ

Để giải bài tập vectơ một cách hiệu quả, học sinh cần lưu ý một số điều sau:

Nắm vững các định nghĩa, tính chất và công thức liên quan đến vectơ.
Vẽ hình minh họa bài toán để dễ dàng hình dung và tìm ra mối liên hệ giữa các yếu tố.
Chọn hệ tọa độ thích hợp để biểu diễn các điểm, vectơ bằng tọa độ.
Sử dụng các phép toán vectơ một cách chính xác và cẩn thận.
Kiểm tra lại kết quả sau khi giải bài toán.

Tài Liệu Tham Khảo

Để học tốt môn Hình học 11 Nâng cao, học sinh có thể tham khảo các tài liệu sau:

Sách giáo khoa Hình học 11 Nâng cao.
Sách bài tập Hình học 11 Nâng cao.
Các trang web học trực tuyến về Hình học.
Các video bài giảng về Hình học.

Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập về vectơ trong hình học không gian. Chúc các em học tốt!

Câu 10 trang 13 SGK Hình học 11 Nâng cao