Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Câu 13 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, tập xác định và tập giá trị để giải quyết.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Xét hàm số a. Chứng minh rằng với mỗi số nguyên k, f(x + k4π) = f(x) với mọi x.
LG a
Chứng minh rằng với mỗi số nguyên \(k\), \(f(x + k4π) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
\(f\left( {x + k4\pi } \right) = \cos \frac{{x + k4\pi }}{2}\)
\(= \cos \left( {{x \over 2} + k2\pi } \right) \) \(= \cos {x \over 2} = f\left( x \right)\)
LG b
Lập bảng biến thiên của hàm số \(y = \cos {x \over 2}\) trên đoạn \([-2π ; 2π]\).
Lời giải chi tiết:
Bảng biến thiên :
LG c
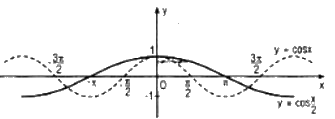
Vẽ đồ thị của các hàm số \(y = \cos x\) và \(y = \cos {x \over 2}\) trong cùng một hệ trục tọa độ vuông góc \(Oxy\).
Lời giải chi tiết:

LG d
Trong mặt phẳng tọa độ \(Oxy\), xét phép biến hình \(F\) biến mỗi điểm \((x ; y)\) thành điểm \((x'; y')\) sao cho \(x'= 2x\) và \(y'= y\). Chứng minh rằng F biến đồ thị của hàm số \(y = \cos x\) thành đồ thị của hàm số \(y = \cos {x \over 2}.\)
Lời giải chi tiết:
Ta có:
\(\left\{ \begin{array}{l}x' = 2x\\y' = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \frac{{x'}}{2}\\y =y'\end{array} \right.\)
Do đó \(y = \cos x\) \( \Leftrightarrow \) \(y' = \cos {{x'} \over 2}\).
Do đó phép biến đổi xác định bởi \((x ; y) ↦ (x' ; y')\) sao cho \(x' = 2x, y'= y\) biến đồ thị hàm số \(y = \cos x\) thành đồ thị hàm số \(y = \cos {x \over 2}.\)

Giải Chi Tiết Câu 13 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xác định tập xác định của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
- Điều kiện xác định của hàm số: Hàm số không xác định khi mẫu số bằng 0, căn thức bậc chẵn có số âm, hoặc logarit có cơ số hoặc biểu thức bên trong logarit không dương.
- Các phép toán trên tập hợp: Giao, hợp, hiệu của các tập hợp.
- Các loại hàm số thường gặp: Hàm số đa thức, hàm số hữu tỉ, hàm số căn thức, hàm số logarit, hàm số lượng giác.
Ví dụ minh họa (giả định nội dung câu 13):
Đề bài: Tìm tập xác định của hàm số f(x) = √(2x - 1) / (x - 3)
Lời giải:
- Điều kiện 1: Căn thức bậc chẵn phải không âm: 2x - 1 ≥ 0 => x ≥ 1/2
- Điều kiện 2: Mẫu số khác 0: x - 3 ≠ 0 => x ≠ 3
- Kết hợp hai điều kiện: x ≥ 1/2 và x ≠ 3
- Vậy tập xác định của hàm số là: D = [1/2; 3) ∪ (3; +∞)
Các Dạng Bài Tập Liên Quan
Ngoài việc tìm tập xác định, học sinh có thể gặp các dạng bài tập liên quan như:
- Tìm tập giá trị của hàm số: Xác định khoảng giá trị mà hàm số có thể đạt được.
- Xác định tính đơn điệu của hàm số: Xác định hàm số đồng biến hay nghịch biến trên một khoảng nào đó.
- Vẽ đồ thị hàm số: Biểu diễn hàm số trên mặt phẳng tọa độ.
Mẹo Giải Bài Tập
Để giải các bài tập về tập xác định một cách hiệu quả, bạn nên:
- Đọc kỹ đề bài: Xác định rõ hàm số và các điều kiện liên quan.
- Liệt kê các điều kiện xác định: Ghi rõ các điều kiện cần thiết để hàm số xác định.
- Giải các bất phương trình hoặc phương trình: Tìm các giá trị của x thỏa mãn các điều kiện xác định.
- Kết hợp các điều kiện: Tìm giao của các tập hợp nghiệm để xác định tập xác định của hàm số.
Luyện Tập Thêm
Để củng cố kiến thức, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. tusach.vn cung cấp nhiều bài tập và lời giải chi tiết để bạn tham khảo.
Bảng Tổng Hợp Các Công Thức Quan Trọng
| Công Thức | Mô Tả |
|---|---|
| √(x) | Căn bậc hai của x, x ≥ 0 |
| loga(x) | Logarit cơ số a của x, x > 0, a > 0, a ≠ 1 |
Hy vọng với lời giải chi tiết và các kiến thức bổ trợ trên, bạn sẽ hiểu rõ hơn về Câu 13 trang 17 SGK Đại số và Giải tích 11 Nâng cao và tự tin giải quyết các bài tập tương tự.