Giải Câu 8 Trang 121 SGK Hình Học 11 Nâng Cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 8 trang 121 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian.
tusach.vn sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
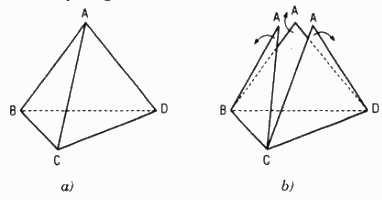
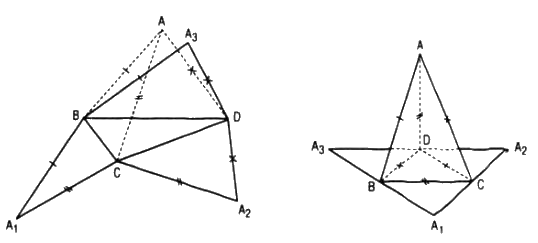
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
Giải Chi Tiết Câu 8 Trang 121 SGK Hình Học 11 Nâng Cao
Câu 8 trang 121 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ để chứng minh một đẳng thức vectơ. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ.
Đề Bài Câu 8 Trang 121 SGK Hình Học 11 Nâng Cao
Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của đoạn thẳng AC. Chứng minh rằng: overrightarrow{AI} = \frac{1}{2} (overrightarrow{AB} +overrightarrow{AD})
Lời Giải Chi Tiết
Để chứng minh đẳng thức vectơ trên, chúng ta sẽ sử dụng các quy tắc cộng, trừ vectơ và tính chất trung điểm của đoạn thẳng.
- Phân tích vectơ AI: Vì I là trung điểm của AC, ta có overrightarrow{AI} = \frac{1}{2} \overrightarrow{AC}.
- Phân tích vectơ AC: Áp dụng quy tắc cộng vectơ, ta có overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}.
- Phân tích vectơ BC: Vì ABCD là hình hộp, nên overrightarrow{BC} = \overrightarrow{AD}.
- Thay thế và rút gọn: Thay overrightarrow{BC} = \overrightarrow{AD} vào biểu thức của overrightarrow{AC}, ta được overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}.
- Kết luận: Thay overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD} vào biểu thức của overrightarrow{AI}, ta được overrightarrow{AI} = \frac{1}{2} (\overrightarrow{AB} + \overrightarrow{AD}). Vậy đẳng thức được chứng minh.
Lưu Ý Quan Trọng
- Nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực.
- Hiểu rõ tính chất trung điểm của đoạn thẳng.
- Sử dụng hình vẽ để minh họa và hỗ trợ quá trình giải bài tập.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Bài 9 trang 121 SGK Hình học 11 Nâng cao
- Bài 10 trang 121 SGK Hình học 11 Nâng cao
Tổng Kết
Hy vọng với lời giải chi tiết này, các em đã hiểu rõ cách giải Câu 8 trang 121 SGK Hình học 11 Nâng cao. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong môn học.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi tại tusach.vn. Chúng tôi luôn sẵn sàng hỗ trợ các em!
| Khái niệm | Giải thích |
|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Quy tắc cộng vectơ | Để cộng hai vectơ, ta vẽ vectơ thứ nhất, rồi vẽ vectơ thứ hai bắt đầu từ điểm cuối của vectơ thứ nhất. Vectơ tổng là vectơ nối điểm đầu của vectơ thứ nhất với điểm cuối của vectơ thứ hai. |