Giải Câu 20 Trang 55 SGK Hình Học 11 Nâng Cao

Câu 20 trang 55 SGK Hình học 11 Nâng cao

Giải Câu 20 Trang 55 SGK Hình Học 11 Nâng Cao

Bài tập Câu 20 trang 55 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên ba cạnh AB, CD, BC. Hãy xác định giao điểm S của mp(PQR) với cạnh AD nếu:

LG a

PR // AC

Phương pháp giải:

- Tìm giao tuyến của (PQR) với (ACD).

Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì chúng cắt nhau theo giao tuyến song song với đường thẳng đã cho.

- Tìm giao điểm S của AD với giao tuyến trên.

Lời giải chi tiết:

Trường hợp PR // AC

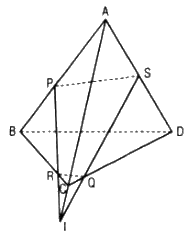
Câu 20 trang 55 SGK Hình học 11 Nâng cao 1

Ta có: \(\left\{ \begin{array}{l}PR \subset \left( {PQR} \right)\\AC \subset \left( {ACD} \right)\\PR//AC\\Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\end{array} \right. \) \(\Rightarrow \left( {PQR} \right) \cap \left( {ACD} \right) = Qt//AC\)

Trong (ACD), gọi S = Qt ∩ AD thì S = AD ∩ (PQR).

LG b

PR cắt AC

Lời giải chi tiết:

Trường hợp PR cắt AC

Câu 20 trang 55 SGK Hình học 11 Nâng cao 1

Trong (ABC), gọi I = PR ∩ AC

\( \Rightarrow \left\{ \begin{array}{l}I \in AC \subset \left( {ACD} \right)\\I \in PR \subset \left( {PQR} \right)\end{array} \right.\)\( \Rightarrow I \in \left( {ACD} \right) \cap \left( {PQR} \right)\)

Mà \( Q\in \left( {ACD} \right) \cap \left( {PQR} \right)\)

⇒ (PQR) ∩ (ACD) = QI

Trong mp(ACD) ta có

S = QI ∩ AD thì S = AD ∩ (PQR).

Giải Chi Tiết Câu 20 Trang 55 SGK Hình Học 11 Nâng Cao

Câu 20 trang 55 SGK Hình học 11 Nâng cao thường xoay quanh việc xác định mối quan hệ giữa đường thẳng và mặt phẳng, hoặc giữa hai mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:

Đường thẳng song song với mặt phẳng: Một đường thẳng song song với một mặt phẳng khi và chỉ khi nó song song với mọi đường thẳng nằm trong mặt phẳng đó.
Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng khi và chỉ khi nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
Góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng vuông góc với cả hai mặt phẳng đó.

Phân Tích Bài Toán Câu 20 Trang 55 (Ví dụ minh họa)

Giả sử bài toán yêu cầu chứng minh một đường thẳng song song với một mặt phẳng. Để giải quyết, ta có thể sử dụng các phương pháp sau:

Chứng minh đường thẳng song song với một đường thẳng nào đó nằm trong mặt phẳng: Nếu đường thẳng d song song với đường thẳng d' nằm trong mặt phẳng (P), thì d song song với (P).
Chứng minh hai mặt phẳng chứa đường thẳng song song: Nếu hai mặt phẳng (P) và (Q) chứa hai đường thẳng song song d và d' tương ứng, thì (P) và (Q) song song.

Lời Giải Chi Tiết (Ví dụ minh họa)

(Ở đây sẽ là lời giải chi tiết của bài toán cụ thể, bao gồm các bước giải, các công thức sử dụng và giải thích rõ ràng.)

Các Dạng Bài Tập Liên Quan

Ngoài Câu 20 trang 55, học sinh có thể gặp các dạng bài tập tương tự như:

Xác định góc giữa đường thẳng và mặt phẳng.
Xác định góc giữa hai mặt phẳng.
Chứng minh sự vuông góc giữa đường thẳng và mặt phẳng.
Chứng minh sự vuông góc giữa hai mặt phẳng.

Mẹo Giải Bài Tập Hình Học 11 Nâng Cao

Để giải tốt các bài tập Hình học 11 Nâng cao, học sinh nên:

Nắm vững các định nghĩa, định lý và tính chất cơ bản.
Vẽ hình chính xác và rõ ràng.
Sử dụng các phương pháp chứng minh phù hợp.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Bảng Tổng Hợp Các Công Thức Quan Trọng

Công Thức	Mô Tả
d // (P)	Đường thẳng d song song với mặt phẳng (P)
d ⊥ (P)	Đường thẳng d vuông góc với mặt phẳng (P)
sin(α)	Góc giữa đường thẳng và mặt phẳng

Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải quyết Câu 20 trang 55 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các em học tốt!

Truy cập tusach.vn để xem thêm nhiều tài liệu học tập và giải bài tập Hình học 11 Nâng cao.

Câu 20 trang 55 SGK Hình học 11 Nâng cao