Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 22 Trang 30
Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và chính xác cho Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập, nắm vững kiến thức và đạt kết quả tốt trong môn Toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, dễ hiểu và phù hợp với chương trình học của các bạn học sinh.
Tính các góc của tam giác ABC
Đề bài
Tính các góc của tam giác \(ABC\), biết \(AB = \sqrt 2 cm\), \(AC =\sqrt 3 cm\) và đường cao \(AH = 1cm\). (Gợi ý : Xét trường hợp \(B, C\) nằm khác phía đối với \(H\) và trường hợp \(B, C\) nằm cùng phía đối với \(H\)).
Lời giải chi tiết
Ta xét hai trường hợp :
a/ \(B\) và \(C\) nằm khác phía đối với \(H\)
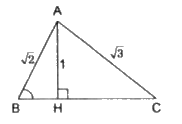
Trong tam giác vuông \(ABH\) ta có :
\(\sin B = {{AH} \over {AB}} = {1 \over {\sqrt 2 }}\)
Suy ra \(\widehat B = 45^\circ \) (chú ý rằng góc \(B\) nhọn)
Trong tam giác \(ACH\) ta có :
\(\sin C = {{AH} \over {AC}} = {1 \over {\sqrt 3 }},\) suy ra \(\widehat C \approx 35^\circ 15'52\)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 99^\circ 44'8\)
b/ \(B\) và \(C\) nằm cùng phía đối với \(H\)
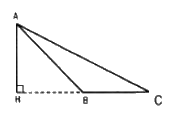
Tương tự như trên ta có:
\(\sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{1}{{\sqrt 2 }}\) \( \Rightarrow \widehat {ABH} = {45^0}\)
\(\eqalign{& \widehat {ABC} = 180^\circ - \widehat {ABH} \cr&= 180^\circ - 45^\circ = 135^\circ \cr } \)
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{1}{{\sqrt 3 }}\) \( \Rightarrow \widehat {ACH} = {35^0}15'52''\)
Từ đó \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right) \approx 9^\circ 44'8\)
Giải Chi Tiết Câu 22 Trang 30 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 22 trang 30 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến các chủ đề về hàm số, đồ thị hàm số, hoặc các bài toán về phương trình, bất phương trình. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững kiến thức cơ bản về các khái niệm và công thức liên quan.
Phân Tích Đề Bài và Xác Định Yêu Cầu
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta tránh được những sai sót không đáng có và tìm ra phương pháp giải phù hợp.
Ví Dụ Minh Họa (Giả sử đề bài là về tìm tập xác định của hàm số)
Đề bài: Tìm tập xác định của hàm số f(x) = √(x² - 4x + 3)
Lời giải:
- Để hàm số f(x) xác định, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0: x² - 4x + 3 ≥ 0
- Giải bất phương trình: x² - 4x + 3 = (x - 1)(x - 3) ≥ 0
- Xét dấu (x - 1)(x - 3):
- x < 1: (x - 1) < 0, (x - 3) < 0 => (x - 1)(x - 3) > 0
- 1 < x < 3: (x - 1) > 0, (x - 3) < 0 => (x - 1)(x - 3) < 0
- x > 3: (x - 1) > 0, (x - 3) > 0 => (x - 1)(x - 3) > 0
- Vậy, tập xác định của hàm số là: D = (-∞; 1] ∪ [3; +∞)
Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải
Trong SGK Đại số và Giải tích 11 Nâng cao, Câu 22 trang 30 có thể thuộc một trong các dạng bài tập sau:
- Tìm tập xác định của hàm số: Cần xét các điều kiện để hàm số có nghĩa (ví dụ: mẫu số khác 0, biểu thức dưới dấu căn không âm, logarit có cơ số lớn hơn 0 và khác 1).
- Xác định tính đơn điệu của hàm số: Sử dụng đạo hàm để xét dấu và kết luận về tính đơn điệu.
- Giải phương trình, bất phương trình: Áp dụng các phương pháp giải phương trình, bất phương trình đã học.
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: Sử dụng đạo hàm để tìm cực trị và so sánh với các giá trị tại biên.
Lưu Ý Quan Trọng Khi Giải Bài Tập
Để giải bài tập một cách chính xác và hiệu quả, bạn cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Nắm vững kiến thức cơ bản về các khái niệm và công thức liên quan.
- Sử dụng các phương pháp giải phù hợp.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn - Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn đồng hành cùng bạn trên con đường học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các mẹo giải bài tập hữu ích. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng Tổng Hợp Các Công Thức Liên Quan (Ví dụ)
| Công Thức | Mô Tả |
|---|---|
| f'(x) | Đạo hàm của hàm số f(x) |
| Δ = b² - 4ac | Biệt thức của phương trình bậc hai |