Giải Câu 44 Trang 47 SGK Đại số và Giải tích 11 Nâng cao
Bài tập Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
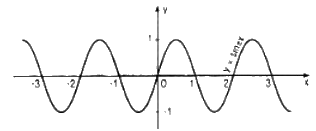
Xét hàm số y = f(x) = sinπx.
Giải Chi Tiết Câu 44 Trang 47 SGK Đại số và Giải tích 11 Nâng cao
Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao yêu cầu chúng ta xét hàm số và tìm các yếu tố liên quan đến hàm số đó. Để giải quyết bài toán này, chúng ta cần nắm vững kiến thức về:
- Tập xác định của hàm số: Tìm các giá trị của x mà hàm số có nghĩa.
- Tính đơn điệu của hàm số: Xác định hàm số đồng biến hay nghịch biến trên các khoảng xác định.
- Cực trị của hàm số: Tìm các điểm cực đại, cực tiểu của hàm số.
- Đồ thị hàm số: Vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
Phân tích đề bài và phương pháp giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Sau đó, lựa chọn phương pháp giải phù hợp. Thông thường, để giải các bài toán về hàm số, chúng ta có thể sử dụng các phương pháp sau:
- Phương pháp xét dấu: Sử dụng để xác định khoảng đồng biến, nghịch biến của hàm số.
- Phương pháp tìm đạo hàm: Sử dụng để tìm cực trị của hàm số.
- Phương pháp vẽ đồ thị: Sử dụng để trực quan hóa hàm số và kiểm tra kết quả.
Lời giải chi tiết Câu 44 trang 47
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm tập xác định, khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số.)
1. Tập xác định: Hàm số y = x3 - 3x2 + 2 xác định trên tập số thực R.
2. Đạo hàm: y' = 3x2 - 6x
3. Tìm cực trị:
- y' = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
- Xét dấu y':
- x < 0: y' > 0 (hàm số đồng biến)
- 0 < x < 2: y' < 0 (hàm số nghịch biến)
- x > 2: y' > 0 (hàm số đồng biến)
- Vậy hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
4. Khoảng đồng biến, nghịch biến:
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
Lưu ý khi giải bài tập
Khi giải các bài tập về hàm số, cần lưu ý những điều sau:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Nắm vững kiến thức về hàm số, đạo hàm và các phép biến đổi hàm số.
- Sử dụng các phương pháp giải phù hợp.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập. Ngoài ra, các em có thể tham khảo các tài liệu ôn thi THPT Quốc gia để nắm vững kiến thức và kỹ năng giải bài tập.
Tusach.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao và tự tin giải các bài tập tương tự.