Giải Câu 2 Trang 91 SGK Hình Học 11 Nâng Cao

Câu 2 trang 91 SGK Hình học 11 Nâng cao

Giải Câu 2 Trang 91 SGK Hình Học 11 Nâng Cao

Câu 2 trang 91 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.

Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.

Cho hình chóp S.ABCD.

Đề bài

Cho hình chóp S.ABCD.

a. Chứng minh rằng nếu ABCD là hình bình hành thì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \). Điều ngược lại có đúng không ?

b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \)

Lời giải chi tiết

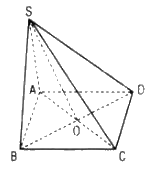
Câu 2 trang 91 SGK Hình học 11 Nâng cao 1

a. Ta có:

\(\eqalign{ & \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \cr & \Leftrightarrow \overrightarrow {SB} - \overrightarrow {SC} = \overrightarrow {SA} - \overrightarrow {SD} \cr&\Leftrightarrow \overrightarrow {CB} = \overrightarrow {DA} \cr} \)

⇔ ABCD là hình bình hành.

b. Ta có:

\(\eqalign{ & \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} \cr& + \overrightarrow {SO} + \overrightarrow {OC} + \overrightarrow {SO} + \overrightarrow {OD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \,\,\left( * \right) \cr} \)

Nếu ABCD là hình bình hành thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) suy ra

\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) (do (*))

Ngược lại, giả sử \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} ,\) ta có (*).

Gọi M, N lần lượt là trung điểm của AC, BD thì :

\(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {OM} ,\overrightarrow {OB} + \overrightarrow {OD} = 2\overrightarrow {ON} \)

Từ (*) suy ra \(2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 ,\) điều này chứng tỏ O, M, N thẳng hàng

Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành.

Giải Chi Tiết Câu 2 Trang 91 SGK Hình Học 11 Nâng Cao

Câu 2 trang 91 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, các phép toán vectơ, điều kiện đồng phẳng của ba vectơ, và phương trình mặt phẳng.

Nội Dung Bài Toán

Thông thường, câu 2 trang 91 sẽ yêu cầu học sinh chứng minh một đẳng thức vectơ, xác định mối quan hệ giữa các vectơ, hoặc tìm phương trình của một mặt phẳng thỏa mãn một điều kiện nào đó. Bài toán có thể liên quan đến các khái niệm như vectơ pháp tuyến, vectơ chỉ phương, góc giữa hai vectơ, và khoảng cách từ một điểm đến một mặt phẳng.

Phương Pháp Giải

Để giải quyết bài toán này một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:

Phân tích bài toán: Đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
Sử dụng các công thức và định lý: Áp dụng các công thức và định lý liên quan đến vectơ, đường thẳng và mặt phẳng để thiết lập các mối quan hệ giữa các yếu tố trong bài toán.
Biến đổi đại số: Thực hiện các phép biến đổi đại số để đơn giản hóa biểu thức và tìm ra kết quả.
Kiểm tra lại kết quả: Sau khi tìm được kết quả, hãy kiểm tra lại để đảm bảo tính chính xác.

Ví Dụ Minh Họa (Giả định một dạng bài tập phổ biến)

Đề bài: Cho bốn điểm A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6). Chứng minh rằng bốn điểm A, B, C, D đồng phẳng.

Lời giải:

Để chứng minh bốn điểm A, B, C, D đồng phẳng, ta cần chứng minh rằng ba vectơ AB, AC, và AD đồng phẳng. Điều này tương đương với việc chứng minh rằng tích hỗn hợp của ba vectơ này bằng 0.

Ta có:

AB = (2-1; 3-2; 4-3) = (1; 1; 1)
AC = (3-1; 4-2; 5-3) = (2; 2; 2)
AD = (4-1; 5-2; 6-3) = (3; 3; 3)

Tích hỗn hợp của AB, AC, và AD là:

[AB, AC, AD] = AB . (AC x AD)

Tính tích có hướng AC x AD:

AC x AD = (2*3 - 2*3; 2*3 - 2*3; 2*3 - 2*3) = (0; 0; 0)

Do đó, [AB, AC, AD] = AB . (0; 0; 0) = 0

Vậy, bốn điểm A, B, C, D đồng phẳng.

Lưu Ý Quan Trọng

Khi giải các bài toán về đường thẳng và mặt phẳng, bạn cần chú ý đến việc sử dụng đúng các công thức và định lý. Ngoài ra, việc vẽ hình minh họa có thể giúp bạn hiểu rõ hơn về bài toán và tìm ra lời giải một cách dễ dàng hơn.

Tusach.vn - Nguồn Tài Liệu Học Tập Toán Học Uy Tín

Tusach.vn là một website cung cấp tài liệu học tập Toán học chất lượng cao, bao gồm giải bài tập SGK, đề thi thử, và các bài giảng trực tuyến. Chúng tôi luôn cập nhật những thông tin mới nhất và hữu ích nhất để giúp bạn học tốt môn Toán.

Câu 2 trang 91 SGK Hình học 11 Nâng cao