Giải Câu 5 Trang 9 SGK Hình Học 11 Nâng Cao

Câu 5 trang 9 SGK Hình học 11 Nâng cao

Giải Câu 5 Trang 9 SGK Hình Học 11 Nâng Cao

Chào mừng các em học sinh đến với lời giải chi tiết Câu 5 trang 9 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học lớp 11, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ cơ bản.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải dễ hiểu nhất.

Trong mặt phẳng tọa độ ,

LG a

Cho hai điểm \(M\left( {{x_1};{y_1}} \right),\,N\left( {{x_2};{y_2}} \right)\) và gọi M', N' lần lượt là ảnh của M,N qua phép F. Hãy tìm tọa độ của M' và N'.

Lời giải chi tiết:

M’ có tọa độ \({(x_1'},{\rm{ }}y{_1}')\) với \(\left\{ {\matrix{{x{'_1} = {x_1}\cos \alpha - {y_1}\sin \alpha + a} \cr {y{'_1} = {x_1}\sin \alpha + {y_1}\cos \alpha + b} \cr} } \right.\)

N’ có tọa độ \({(x_2'},{\rm{ }}y{_2}')\) với \(\left\{ {\matrix{{x{'_2} = {x_2}\cos \alpha - {y_2}\sin \alpha + a} \cr {y{'_2} = {x_2}\sin \alpha + {y_2}\cos \alpha + b} \cr} } \right.\)

LG b

Tính khoảng cách d giữa M và N; khoảng cách d' giữa M' và N'

Lời giải chi tiết:

Ta có \(d=MN=\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

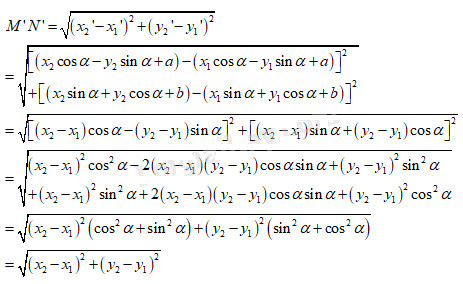
Câu 5 trang 9 SGK Hình học 11 Nâng cao 1

LG c

Phép F có phải là phép dời hình hay không ?

Lời giải chi tiết:

Từ câu b suy ra \(MN=M'N'\) do đó \(F\) là phép dời hình.

LG d

Khi \(\alpha = 0\), chứng tỏ rằng F là phép tịnh tiến

Lời giải chi tiết:

Khi \(\alpha=0\) thì:

\(\begin{array}{l}\left\{ \begin{array}{l}x' = x\cos 0 - y\sin 0 + a\\y' = x\sin 0 + y\cos 0 + b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x' = x.1 - y.0 + a\\y' = x.0 + y.1 + b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\end{array}\)

Vậy \(F\) là phép tịnh tiến vectơ \(\overrightarrow u \left( {a;b} \right).\)

Giải Chi Tiết Câu 5 Trang 9 SGK Hình Học 11 Nâng Cao

Câu 5 trang 9 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ, đặc biệt là các phép toán cộng, trừ vectơ và phép nhân vectơ với một số thực. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và tính chất cơ bản sau:

Vectơ: Một đoạn thẳng có hướng. Vectơ được xác định bởi điểm gốc và điểm cuối.
Phép cộng vectơ: Quy tắc hình bình hành hoặc quy tắc tam giác.
Phép trừ vectơ:AB - AC = CB
Phép nhân vectơ với một số thực:k.AB là một vectơ có cùng hướng với AB nếu k > 0 và ngược hướng nếu k < 0. Độ dài của k.AB là |k| lần độ dài của AB.

Phân tích bài toán Câu 5 Trang 9 SGK Hình Học 11 Nâng Cao

Để giải Câu 5 trang 9, chúng ta cần đọc kỹ đề bài, xác định các vectơ đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta tính toán một vectơ mới dựa trên các vectơ đã cho, hoặc chứng minh một đẳng thức vectơ nào đó.

Lời giải chi tiết Câu 5 Trang 9 SGK Hình Học 11 Nâng Cao (Ví dụ minh họa - cần thay thế bằng nội dung cụ thể của đề bài)

Giả sử đề bài yêu cầu: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: 2AM = AB + AC

Vẽ hình: Vẽ tam giác ABC và trung điểm M của BC.
Phân tích:AM là trung tuyến của tam giác ABC. Ta cần chứng minh mối quan hệ giữa AM và AB, AC.
Chứng minh:
Ta có: BM = MC (M là trung điểm của BC)
AB + AC = AB + (AM + MC) = AB + AM + MC
Vì BM = MC nên MC = -BM
AB + AC = AB + AM - BM = AB + AM - (BC - AB) = 2AB + AM - BC
Tuy nhiên, cách tiếp cận này chưa đúng. Ta sử dụng quy tắc hình bình hành:
AB + AC = AD (với D là đỉnh thứ tư của hình bình hành AB CD)
Ta thấy rằng AD và 2AM là hai đường chéo của hình bình hành. Do đó, 2AM = AB + AC (đpcm)

Mẹo giải nhanh và lưu ý

Luôn vẽ hình để hình dung rõ bài toán.
Sử dụng quy tắc hình bình hành hoặc quy tắc tam giác để cộng, trừ vectơ.
Chú ý đến dấu của số thực khi nhân vectơ với một số thực.
Kiểm tra lại kết quả sau khi giải xong.

Các bài tập tương tự

Để củng cố kiến thức về vectơ, các em có thể tham khảo thêm các bài tập tương tự trong SGK Hình học 11 Nâng cao và các tài liệu luyện tập khác.

Tusach.vn hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về Câu 5 trang 9 SGK Hình học 11 Nâng cao và tự tin hơn trong quá trình học tập. Chúc các em học tốt!

Câu 5 trang 9 SGK Hình học 11 Nâng cao