Câu 15 trang 195 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 15 Trang 195
Chào mừng bạn đến với tusach.vn! Chúng tôi cung cấp lời giải chi tiết và chính xác cho Câu 15 trang 195 SGK Đại số và Giải tích 11 Nâng cao. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập, nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, dễ hiểu và phù hợp với chương trình học của các bạn học sinh.
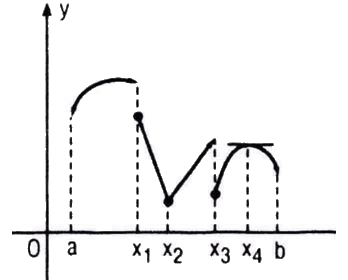
Hình 5.5 là đồ thị của hàm số y = f(x) xác
Đề bài
Hình 5.5 là đồ thị của hàm số y = f(x) xác định trên khoảng (a ; b). Dựa vào hình vẽ, hãy cho biết tại mỗi điểm x1, x2, x3 và x4 :
a. Hàm số có liên tục hay không ?
b. Hàm số có đạo hàm hay không ? Hãy tính đạo hàm nếu có.
Lời giải chi tiết
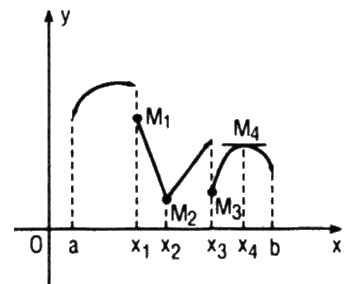
Căn cứ vào hình ta nhận thấy :
+ Hàm số đã cho gián đoạn tại các điểm x1 và x3; vì đồ thị hàm số bị ngắt quãng khi đi qua các điểm M1 và M3.
+ Hàm số đã cho liên tục tại các điểm x2 và x4; vì đồ thị hàm số là đường “liền nét” khi đi qua các điểm M2 và M4
+ Hàm số không có đạo hàm tại điểm x2; vì điểm M2 đồ thị là đường “gấp khúc” (và hiển nhiên tại đó không có tiếp tuyến của đồ thị hàm số), giống như đồ thị hàm số \(y = |x|\).
+ Hàm số có đạo hàm tại điểm M4 và \(f'\left( {{x_4}} \right) = 0;\) vì tại điểm M4 đồ thị của hàm số có tiếp tuyến và tiếp tuyến này song song với trục hoành.
Giải Chi Tiết Câu 15 Trang 195 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 15 trang 195 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về hàm số, đạo hàm và các ứng dụng của đạo hàm. Bài tập này thường yêu cầu học sinh tìm cực trị của hàm số, khảo sát hàm số hoặc giải các bài toán liên quan đến tối ưu hóa.
Nội Dung Bài Tập
Để giải quyết Câu 15 trang 195, trước tiên, chúng ta cần xác định rõ yêu cầu của bài tập. Thông thường, bài tập sẽ cho một hàm số và yêu cầu tìm:
- Cực trị của hàm số: Tìm các điểm mà hàm số đạt giá trị lớn nhất hoặc nhỏ nhất trên một khoảng xác định.
- Khảo sát hàm số: Xác định các khoảng đồng biến, nghịch biến, điểm uốn, tiệm cận và vẽ đồ thị hàm số.
- Bài toán tối ưu hóa: Tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số trong một miền xác định, thường liên quan đến các ứng dụng thực tế.
Phương Pháp Giải
Để giải quyết các bài tập này, chúng ta cần áp dụng các kiến thức và kỹ năng sau:
- Tính đạo hàm: Tính đạo hàm bậc nhất và đạo hàm bậc hai của hàm số.
- Tìm điểm cực trị: Giải phương trình đạo hàm bậc nhất bằng 0 để tìm các điểm nghi ngờ là cực trị. Sau đó, sử dụng đạo hàm bậc hai để xác định loại cực trị (cực đại hoặc cực tiểu).
- Khảo sát hàm số: Dựa vào dấu của đạo hàm bậc nhất để xác định các khoảng đồng biến, nghịch biến. Dựa vào đạo hàm bậc hai để xác định điểm uốn.
- Tìm tiệm cận: Xác định các tiệm cận đứng, tiệm cận ngang và tiệm cận xiên của hàm số.
- Vẽ đồ thị: Sử dụng các thông tin đã tìm được để vẽ đồ thị hàm số.
Ví Dụ Minh Họa
Giả sử bài tập yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2. Chúng ta sẽ thực hiện các bước sau:
- Tính đạo hàm: f'(x) = 3x2 - 6x
- Tìm điểm cực trị: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
- Xác định loại cực trị: f''(x) = 6x - 6. Tại x = 0, f''(0) = -6 < 0, nên x = 0 là điểm cực đại. Tại x = 2, f''(2) = 6 > 0, nên x = 2 là điểm cực tiểu.
- Tính giá trị cực trị: f(0) = 2 (cực đại), f(2) = -2 (cực tiểu).
Vậy, hàm số f(x) đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Lưu Ý Quan Trọng
Khi giải các bài tập về hàm số, đạo hàm và ứng dụng của đạo hàm, bạn cần:
- Nắm vững các định nghĩa và tính chất của hàm số, đạo hàm.
- Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
- Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
Tusach.vn - Đồng Hành Cùng Bạn
Tusach.vn luôn sẵn sàng hỗ trợ bạn trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu và chính xác cho tất cả các bài tập trong SGK Đại số và Giải tích 11 Nâng cao. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc bạn học tập tốt!