Câu 1 trang 34 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 1 trang 34 SGK Hình học 11 Nâng cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 1 trang 34 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình Hình học không gian, tập trung vào việc ôn tập kiến thức về đường thẳng và mặt phẳng trong không gian.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Cho hai đường tròn (O ; R), (O’ ; R’) và một đường thẳng d
Đề bài
Cho hai đường tròn (O ; R), (O’ ; R’) và một đường thẳng d
a. Tìm hai điểm M, N lần lượt nằm trên hai đường tròn đó sao cho d là đường trung trực của đoạn thẳng MN
b. Xác định điểm I trên d sao cho tiếp tuyến IT của (O ; R) và tiếp tuyến IT’ của (O’ ; R’) hợp thành các góc mà d là một trong các đường phân giác của các góc đó
Lời giải chi tiết
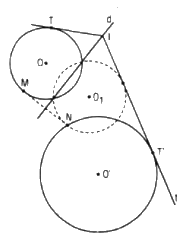
a. Gọi (O1 ; R) là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đd
Giao điểm (nếu có) của hai đường tròn (O1 ; R) và (O’ ; R’) chính là điểm N cần tìm, điểm M là điểm đối xứng với N qua d
b. Vẫn gọi (O1 ; R) như trên và I là điểm cần tìm thì IT’ là tiếp tuyến chung của hai đường tròn (O1 ; R) và (O’ ; R’)
Suy ra cách dựng: Vẽ tiếp tuyến chung t (nếu có) của hai đường tròn (O1 ; R) và (O’ ; R’)
Giao điểm (nếu có) của t và d chính là điểm I cần tìm
Khi đó tiếp tuyến IT’ chính là t còn đường thẳng đối xứng với IT’ qua d là tiếp tuyến IT của (O ; R)
Giải chi tiết Câu 1 trang 34 SGK Hình học 11 Nâng cao
Câu 1 trang 34 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng, cũng như các tính chất của đường thẳng song song, đường thẳng vuông góc với mặt phẳng để giải quyết. Dưới đây là lời giải chi tiết:
Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD) và SA = a. Gọi M là trung điểm của cạnh CD.
- Chứng minh rằng BD vuông góc với AM.
- Tính góc giữa đường thẳng SM và mặt phẳng (ABCD).
- Tính khoảng cách từ điểm C đến mặt phẳng (SAD).
Lời giải:
a) Chứng minh BD vuông góc với AM:
Ta có:
- BD vuông góc với AD (do ABCD là hình vuông).
- BD vuông góc với CM (do CM vuông góc với CD và ABCD là hình vuông).
- BD vuông góc với (ADM) (do BD vuông góc với hai đường thẳng AD và CM cắt nhau tại M trong mặt phẳng (ADM)).
- AM nằm trong mặt phẳng (ADM) nên BD vuông góc với AM.
Vậy BD vuông góc với AM.
b) Tính góc giữa đường thẳng SM và mặt phẳng (ABCD):
Vì SA vuông góc với mặt phẳng (ABCD) nên góc giữa đường thẳng SM và mặt phẳng (ABCD) chính là góc SMO, với O là hình chiếu của M lên AB.
Ta có:
- MO = AD/2 = a/2
- SO = √(SA2 + AO2) = √(a2 + (a/2)2) = a√(5)/2
- tan SMO = SO/MO = (a√(5)/2) / (a/2) = √5
- SMO = arctan(√5) ≈ 65.9°
Vậy góc giữa đường thẳng SM và mặt phẳng (ABCD) là arctan(√5) ≈ 65.9°.
c) Tính khoảng cách từ điểm C đến mặt phẳng (SAD):
Gọi d là khoảng cách từ C đến mặt phẳng (SAD). Ta có:
VCSAD = (1/3) VSAD
VSAD = (1/3) diện tích(SAD) * SA = (1/3) * (1/2 * AD * SA) * SA = (1/6) a3
VCSAD = (1/3) * (1/6) a3 = (1/18) a3
Diện tích tam giác SAD = (1/2) * AD * SA = (1/2) a2
d = (3 * VCSAD) / diện tích(SAD) = (3 * (1/18) a3) / (1/2 a2) = a/3
Vậy khoảng cách từ điểm C đến mặt phẳng (SAD) là a/3.
Lưu ý quan trọng:
Khi giải các bài toán về hình học không gian, việc vẽ hình chính xác và sử dụng các định lý, tính chất một cách linh hoạt là rất quan trọng. Hãy luôn kiểm tra lại các bước giải và đảm bảo tính logic của bài làm.
Tổng kết:
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải Câu 1 trang 34 SGK Hình học 11 Nâng cao. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Đường thẳng vuông góc với mặt phẳng | Đường thẳng tạo với mặt phẳng một góc 90 độ. |
| Góc giữa đường thẳng và mặt phẳng | Góc tạo bởi đường thẳng và hình chiếu của nó trên mặt phẳng. |
| Khoảng cách từ điểm đến mặt phẳng | Độ dài đoạn vuông góc hạ từ điểm xuống mặt phẳng. |