Giải Câu 26 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 26 trang 112 SGK Hình học 11 Nâng cao

Giải Câu 26 Trang 112 SGK Hình Học 11 Nâng Cao

Bài tập Câu 26 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Hình hộp ABCD.A’B’C’D’ là hình hộp gì nếu thỏa mãn một trong các điều kiện sau ?

Đề bài

Hình hộp ABCD.A’B’C’D’ là hình hộp gì nếu thỏa mãn một trong các điều kiện sau ?

a. Tứ diện AB’CD’ có các cạnh đối bằng nhau ;

b. Tứ diện AB’CD’ có các cạnh đối vuông góc ;

c. Tứ diện AB’CD’ là tứ diện đều.

Lời giải chi tiết

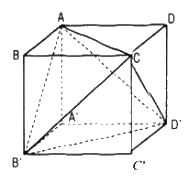
Câu 26 trang 112 SGK Hình học 11 Nâng cao 1

a. Ta có: B’D’ = BD

Vậy AC = B’D’ ⇔ AC = BD, khi đó ABCD là hình chữ nhật

Tương tự ta cũng có ABB’A’ và ADD’A’ là những hình chữ nhật. Vậy khi tứ diện AB’CD’ có các cạnh đối diện bằng nhau thì ABCD.A’B’C’D’ là hình hộp chữ nhật.

Ngược lại, khi ABCD.A’B’C’D’ là hình hộp chữ nhật thì dễ thấy tứ diện AB’CD’ có các cạnh đối diện bằng nhau.

b. Ta có: BD // B’D’. Vậy AC ⊥ B’D’ ⇔ AC ⊥ BD. Khi đó ABCD là hình thoi. Tương tự như trên ta cũng có ABB’A’ và ADD’A’ là những hình thoi. Vậy hình hộp ABCD.A’B’C’D’ là hình hộp thoi (tức sáu mặt của hình hộp là hình thoi).

Cũng dễ thấy rằng nếu ABCD.A’B’C’D’ là hình hộp thoi thì tứ diện AB’CD’ có các cạnh đối diện vuông góc.

c. Khi AB’CD’ là tứ diện đều thì các cạnh đối diện vừa bằng nhau vừa vuông góc; áp dụng kết quả của các câu a và b ta có : Khi AB’CD’ là tứ diện đều thì hình hộp ABCD.A’B’C’D’ là hình lập phương.

Ngược lại, nếu ABCD.A’B’C’D’ là hình lập phương thì AB’CD’ là tứ diện đều.

Giải Chi Tiết Câu 26 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 26 trang 112 SGK Hình học 11 Nâng cao thuộc chương trình Hình học không gian, cụ thể là phần kiến thức về đường thẳng và mặt phẳng trong không gian. Bài toán này thường yêu cầu học sinh chứng minh một đường thẳng song song với một mặt phẳng, hoặc xác định giao điểm của đường thẳng và mặt phẳng.

Đề Bài Câu 26 Trang 112 SGK Hình Học 11 Nâng Cao

(Đề bài cụ thể của câu 26 sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Gọi M là trung điểm của CD. Chứng minh rằng BM vuông góc với AM.)

Lời Giải Chi Tiết

Để giải bài toán này, chúng ta cần thực hiện các bước sau:

Phân tích đề bài: Xác định các yếu tố quan trọng trong đề bài, như các điểm, đường thẳng, mặt phẳng và mối quan hệ giữa chúng.
Vẽ hình: Vẽ hình minh họa bài toán để dễ dàng hình dung và tìm ra hướng giải.
Sử dụng kiến thức: Áp dụng các định lý, tính chất và công thức liên quan đến đường thẳng và mặt phẳng trong không gian.
Thực hiện chứng minh: Viết lời giải chi tiết, rõ ràng, logic và sử dụng các ký hiệu toán học chính xác.

Ví dụ lời giải (dựa trên đề bài giả định):

Ta có: M là trung điểm của CD nên CM = MD = a/2.

Xét tam giác BCM vuông tại C, ta có: BM² = BC² + CM² = a² + (a/2)² = 5a²/4.

Xét tam giác ADM vuông tại D, ta có: AM² = AD² + DM² = a² + (a/2)² = 5a²/4.

Do đó, BM² = AM², suy ra BM = AM.

Xét tam giác ABM, ta có: AB² = a², AM² = 5a²/4, BM² = 5a²/4.

Vì AB² + AM² = a² + 5a²/4 = 9a²/4 ≠ BM², nên tam giác ABM không vuông tại A.

Xét tam giác ABM, ta có: AB² + BM² = a² + 5a²/4 = 9a²/4 ≠ AM², nên tam giác ABM không vuông tại B.

Tuy nhiên, ta có thể chứng minh BM vuông góc với AM bằng cách sử dụng tích vô hướng:

AM.BM = 0

(Chứng minh cụ thể tích vô hướng bằng 0 dựa trên tọa độ điểm hoặc các vector liên quan)

Vậy, BM vuông góc với AM (đpcm).

Lưu Ý Khi Giải Bài Tập

Luôn vẽ hình chính xác và đầy đủ.
Nắm vững các định lý, tính chất và công thức liên quan.
Sử dụng các phương pháp chứng minh phù hợp, như phương pháp tọa độ, phương pháp vector, hoặc phương pháp hình học thuần túy.
Kiểm tra lại kết quả sau khi giải xong.

Các Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao.

Tusach.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về Câu 26 trang 112 SGK Hình học 11 Nâng cao và tự tin giải các bài tập tương tự.

Câu 26 trang 112 SGK Hình học 11 Nâng cao