Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 36 Trang 163
Chào mừng bạn đến với lời giải chi tiết Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao trên tusach.vn.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tìm các giới hạn sau :
LG a
\(\mathop {\lim }\limits_{x \to + \infty } {{{x^3} - 5} \over {{x^2} + 1}}\)
Lời giải chi tiết:
\(\eqalign{& \mathop {\lim }\limits_{x \to + \infty } {{{x^3} - 5} \over {{x^2} + 1}} = \mathop {\lim }\limits_{x \to + \infty } {x}{{{x^2}\left( {1 - {5 \over {{x^3}}}} \right)} \over {{x^2}\left( {1 + {1 \over {{x^2}}}} \right)}} \cr & = \mathop {\lim }\limits_{x \to + \infty } x.{{1 - {5 \over {{x^3}}}} \over {1 + {1 \over {{x^2}}}}} = + \infty \cr & \text{vì}\,\mathop {\lim }\limits_{x \to + \infty } x = + \infty \,\text{và}\,\mathop {\lim }\limits_{x \to + \infty } {{1 - {5 \over {{x^3}}}} \over {1 + {1 \over {{x^2}}}}} = 1 > 0 \cr} \)
Cách khác:
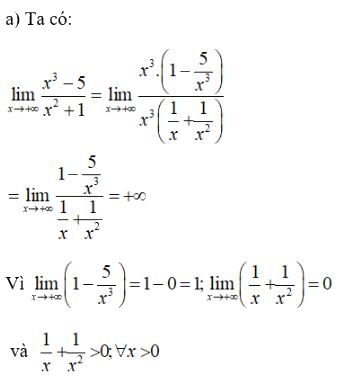
LG b
\(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}}\)
Lời giải chi tiết:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^4}\left( {1 - \frac{1}{{{x^3}}}} \right)} }}{{1 - 2x}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}\sqrt {1 - \frac{1}{{{x^3}}}} }}{{x\left( {\frac{1}{x} - 2} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \left[ {x.\frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}}} \right]\end{array}\)
Ta có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } x = - \infty \\\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}} = \frac{1}{{ - 2}} < 0\end{array}\)
Do đó \(\mathop {\lim }\limits_{x \to - \infty } \left( {x.\frac{{\sqrt {1 - \frac{1}{{{x^3}}}} }}{{\frac{1}{x} - 2}}} \right) = + \infty \)
Vậy \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}}= + \infty \)
Cách khác:
Với mọi \(x < 0\), ta có \({{\sqrt {{x^4} - x} } \over {1 - 2x}} = {{{x^2}\sqrt {1 - {1 \over {{x^3}}}} } \over {1 - 2x}} = {{\sqrt {1 - {1 \over {{x^3}}}} } \over {{1 \over {{x^2}}} - {2 \over x}}}\)
Vì \(\mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {1 \over {{x^3}}}} = 1,\) \(\mathop {\lim }\limits_{x \to - \infty } \left( {{1 \over {{x^2}}} - {2 \over x}} \right) = 0\,\text{ và }\,{1 \over {{x^2}}} - {2 \over x} > 0\) với mọi \(x < 0\)
Nên \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} - x} } \over {1 - 2x}} = + \infty \)
Giải Chi Tiết Câu 36 Trang 163 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học, thường liên quan đến các kiến thức về hàm số, đạo hàm, hoặc các chủ đề khác tùy thuộc vào nội dung cụ thể của bài. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan.
Nội Dung Bài Tập (Ví dụ - cần thay thế bằng nội dung thực tế của câu 36)
Giả sử câu 36 yêu cầu tìm đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1. Đây là một ví dụ minh họa, nội dung thực tế sẽ khác.
Phương Pháp Giải
Để giải bài tập này, chúng ta sẽ sử dụng các quy tắc đạo hàm cơ bản:
- Đạo hàm của xn là nxn-1
- Đạo hàm của một hằng số là 0
- Đạo hàm của một tổng (hoặc hiệu) là tổng (hoặc hiệu) các đạo hàm
Lời Giải Chi Tiết
Áp dụng các quy tắc đạo hàm trên, ta có:
f'(x) = d/dx (x3) - d/dx (2x2) + d/dx (5x) - d/dx (1)
f'(x) = 3x2 - 4x + 5 - 0
f'(x) = 3x2 - 4x + 5
Các Lưu Ý Quan Trọng
- Luôn kiểm tra lại kết quả sau khi tính toán.
- Hiểu rõ các khái niệm và công thức liên quan trước khi bắt đầu giải bài tập.
- Thực hành nhiều bài tập tương tự để củng cố kiến thức.
Bài Tập Tương Tự
Để giúp bạn luyện tập và nắm vững kiến thức, dưới đây là một số bài tập tương tự:
- Tìm đạo hàm của hàm số g(x) = 2x4 + x2 - 3
- Tìm đạo hàm của hàm số h(x) = -x5 + 7x - 2
Tại Sao Nên Chọn tusach.vn?
tusach.vn là một nguồn tài liệu học tập uy tín, cung cấp:
- Lời giải chi tiết, chính xác và dễ hiểu.
- Đội ngũ giáo viên giàu kinh nghiệm.
- Cập nhật liên tục các bài tập mới.
- Giao diện thân thiện, dễ sử dụng.
Kết Luận
Hy vọng lời giải chi tiết Câu 36 trang 163 SGK Đại số và Giải tích 11 Nâng cao trên tusach.vn sẽ giúp bạn hiểu rõ hơn về bài tập và tự tin hơn trong quá trình học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Kiến thức liên quan |
|---|---|
| Đạo hàm | Quy tắc đạo hàm, đạo hàm của hàm đa thức |
| Hàm số | Định nghĩa hàm số, các loại hàm số |