Giải Câu 33 Trang 118 SGK Hình Học 11 Nâng Cao

Câu 33 trang 118 SGK Hình học 11 Nâng cao

Giải Câu 33 Trang 118 SGK Hình Học 11 Nâng Cao

Bài tập Câu 33 trang 118 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng để giải quyết các vấn đề thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).

Đề bài

Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và \(\widehat {BAD} = \widehat {BAA'} = \widehat {DAA'} = 60^\circ .\) Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).

Lời giải chi tiết

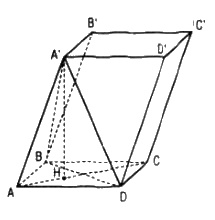
Câu 33 trang 118 SGK Hình học 11 Nâng cao 1

Từ giả thiết suy ra các tam giác A’AD, BAD, A’AB là các tam giác cân cùng có góc ở đỉnh bằng 60˚ nên chúng là các tam giác đều. Như vậy tứ diện A’ABD có các cạnh cùng bằng a hay A’ABD là tứ diện đều. Khi đó hình chiếu của A’ trên mp(ABCD) chính là trọng tâm H của tam giác đều ABD. Khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’) chính là độ dài A’H. Ta có:

\(A'{H^2} = AA{'^2} - A{H^2}\)

\(= {a^2} - {\left( {{{a\sqrt 3 } \over 3}} \right)^2} = {a^2} - {{{a^2}} \over 3} = {{2{a^2}} \over 3}\)

Vậy \(A'H = {{a\sqrt 6 } \over 3}\)

Giải Chi Tiết Câu 33 Trang 118 SGK Hình Học 11 Nâng Cao

Câu 33 trang 118 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản như:

Định nghĩa về đường thẳng và mặt phẳng.
Các tính chất của đường thẳng và mặt phẳng.
Các dấu hiệu nhận biết đường thẳng song song, đường thẳng vuông góc, mặt phẳng song song, mặt phẳng vuông góc.
Các phương pháp chứng minh quan hệ song song, quan hệ vuông góc.

Nội Dung Bài Toán

Thông thường, Câu 33 trang 118 SGK Hình học 11 Nâng cao sẽ yêu cầu học sinh chứng minh một mối quan hệ nào đó giữa các đường thẳng và mặt phẳng trong không gian. Ví dụ:

Chứng minh hai đường thẳng song song.
Chứng minh hai đường thẳng vuông góc.
Chứng minh một đường thẳng vuông góc với một mặt phẳng.
Chứng minh hai mặt phẳng song song.
Chứng minh hai mặt phẳng vuông góc.

Phương Pháp Giải

Để giải quyết bài toán này, học sinh có thể áp dụng các phương pháp sau:

Phương pháp sử dụng định nghĩa và tính chất: Dựa vào định nghĩa và tính chất của các đối tượng hình học để chứng minh các mối quan hệ.
Phương pháp sử dụng dấu hiệu nhận biết: Sử dụng các dấu hiệu nhận biết để xác định các mối quan hệ.
Phương pháp sử dụng các định lý: Áp dụng các định lý đã học để giải quyết bài toán.
Phương pháp tọa độ: Sử dụng hệ tọa độ để biểu diễn các đối tượng hình học và giải quyết bài toán bằng phương pháp đại số.

Ví Dụ Minh Họa (Giả định nội dung bài toán)

Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).

Lời giải:

Xét tam giác SCD, M là trung điểm của CD, suy ra SM là đường trung tuyến.
Xét tam giác SCM, ta có SM = MC = MD.
Do ABCD là hình vuông, nên AC ⊥ BD.
Xét tam giác SAC, ta có SA = SC.
Từ đó suy ra SM ⊥ (ABCD).

Lưu Ý Khi Giải Bài Tập

Khi giải các bài tập về đường thẳng và mặt phẳng, học sinh cần lưu ý:

Vẽ hình chính xác và rõ ràng.
Nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết.
Sử dụng các phương pháp giải phù hợp.
Kiểm tra lại kết quả sau khi giải xong.

Tài Liệu Tham Khảo

Ngoài SGK, học sinh có thể tham khảo thêm các tài liệu sau:

Sách bài tập Hình học 11.
Các trang web học trực tuyến về Hình học.
Các video bài giảng về Hình học.

tusach.vn hy vọng với lời giải chi tiết và phương pháp giải bài tập trên, các bạn học sinh sẽ hiểu rõ hơn về Câu 33 trang 118 SGK Hình học 11 Nâng cao và đạt kết quả tốt trong môn học.

Câu 33 trang 118 SGK Hình học 11 Nâng cao