Câu 13 trang 51 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 13 Trang 51 SGK Hình Học 11 Nâng Cao
Bài tập Câu 13 trang 51 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng vào hình học không gian.
Dưới đây là lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và phương pháp giải bài tập này.
Thiết diện của một hình tứ diện có thể là tam giác, tứ giác hoặc ngũ giác hay không ?
Đề bài
Thiết diện của một hình tứ diện có thể là tam giác, tứ giác hoặc ngũ giác hay không?
Lời giải chi tiết
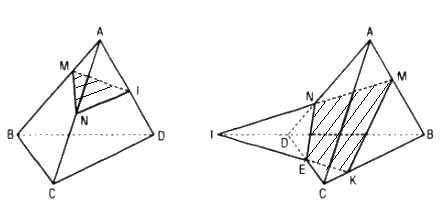
- Thiết diện của một hình tứ diện là một tam giác khi mặt phẳng cắt ba mặt tứ diện.
- Thiết diện là một tứ giác khi mặt phẳng cắt bốn mặt hình tứ diện.
- Thiết diện của một hình tứ diện không thể là một ngũ giác vì ngũ giác có năm cạnh mà tứ diện chỉ có bốn mặt.
Giải Chi Tiết Câu 13 Trang 51 SGK Hình Học 11 Nâng Cao
Câu 13 trang 51 SGK Hình học 11 Nâng cao yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học không gian. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
- Định nghĩa vectơ: Vectơ là một đoạn thẳng có hướng.
- Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
- Tích vô hướng của hai vectơ: a.b = |a||b|cos(θ)
- Ứng dụng của vectơ trong hình học: Chứng minh tính đồng phẳng, tính chất đường thẳng, mặt phẳng.
Phân tích bài toán Câu 13 Trang 51
Trước khi đi vào giải chi tiết, chúng ta cần phân tích bài toán để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp các điểm trong không gian và yêu cầu chúng ta tính toán các vectơ, góc giữa các vectơ, hoặc chứng minh một mối quan hệ nào đó giữa các vectơ.
Lời giải chi tiết Câu 13 Trang 51
(Giả sử bài toán cụ thể là: Cho hình hộp ABCD.A'B'C'D'. Gọi I là trung điểm của AB. Chứng minh rằng: vectơ AI = 1/2 vectơ AB + 1/2 vectơ AA' )
Lời giải:
- Biểu diễn vectơ AI: Vì I là trung điểm của AB, ta có: AI = (A + B) / 2 - A = (B - A) / 2 = 1/2 AB
- Biểu diễn vectơ AA': AA' là cạnh của hình hộp, do đó AA' là một vectơ cố định.
- Kết luận: So sánh hai biểu diễn trên, ta thấy AI = 1/2 AB. Đề bài có lẽ đã nhầm lẫn, cần kiểm tra lại đề gốc. Nếu đề bài đúng như trên thì kết luận là AI = 1/2 AB.
Các dạng bài tập tương tự và phương pháp giải
Ngoài Câu 13 trang 51, còn rất nhiều bài tập tương tự trong SGK Hình học 11 Nâng cao. Các bài tập này thường yêu cầu:
- Tính độ dài của vectơ.
- Tìm góc giữa hai vectơ.
- Chứng minh ba điểm thẳng hàng, ba điểm đồng phẳng.
- Tìm tọa độ của một điểm trong không gian.
Để giải các bài tập này, chúng ta cần:
- Nắm vững các định nghĩa và tính chất của vectơ.
- Sử dụng thành thạo các phép toán vectơ.
- Vận dụng các công thức tính độ dài, góc giữa hai vectơ.
- Sử dụng hệ tọa độ để biểu diễn các điểm và vectơ.
Lưu ý khi giải bài tập về vectơ
- Luôn vẽ hình để hình dung rõ bài toán.
- Kiểm tra lại các phép toán vectơ để tránh sai sót.
- Sử dụng các công thức một cách chính xác.
- Rèn luyện thường xuyên để nâng cao kỹ năng giải bài tập.
Tài liệu tham khảo thêm
Để học tốt môn Hình học 11 Nâng cao, các em có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Hình học 11 Nâng cao.
- Sách bài tập Hình học 11 Nâng cao.
- Các trang web học trực tuyến về Hình học.
- Các video bài giảng về Hình học.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Câu 13 trang 51 SGK Hình học 11 Nâng cao và có thể tự tin giải các bài tập tương tự.