Câu 44 trang 75 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Hình Học 11 Nâng Cao - Câu 44 Trang 75
Câu 44 trang 75 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết các vấn đề thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Vẽ hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn
Đề bài
Vẽ hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn
Lời giải chi tiết
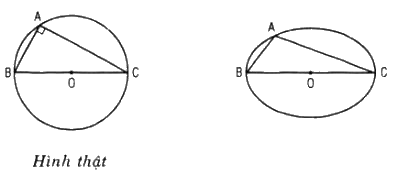
Vẽ elip tâm O là hình biểu diễn của đường tròn đã cho. Lấy B và C là hai điểm trên elip sao cho B, O, C thẳng hàng và một điểm A thuộc elip sao cho A khác B và C. Khi đó, tam giác ABC là hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn.
Giải Chi Tiết Câu 44 Trang 75 SGK Hình Học 11 Nâng Cao
Câu 44 trang 75 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, phương trình đường thẳng, phương trình mặt phẳng và các mối quan hệ giữa chúng.
Đề Bài Câu 44 Trang 75 SGK Hình Học 11 Nâng Cao
(Đề bài cụ thể của câu 44 sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Hướng Dẫn Giải Chi Tiết
Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:
- Bước 1: Xác định các yếu tố cần thiết. Xác định các điểm, vectơ, mặt phẳng liên quan đến bài toán.
- Bước 2: Thiết lập hệ tọa độ. Chọn một hệ tọa độ thích hợp để biểu diễn các điểm và vectơ trong không gian.
- Bước 3: Tìm vectơ chỉ phương của đường thẳng. Xác định vectơ chỉ phương của đường thẳng SC.
- Bước 4: Tìm vectơ pháp tuyến của mặt phẳng. Xác định vectơ pháp tuyến của mặt phẳng (ABCD).
- Bước 5: Tính góc giữa đường thẳng và mặt phẳng. Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin(θ) = |(a.n)| / (||a|| * ||n||), trong đó a là vectơ chỉ phương của đường thẳng, n là vectơ pháp tuyến của mặt phẳng, và θ là góc giữa đường thẳng và mặt phẳng.
Lời Giải Chi Tiết
(Lời giải chi tiết, bao gồm các phép tính cụ thể và giải thích từng bước, sẽ được trình bày ở đây. Ví dụ:)
Chọn hệ tọa độ Oxyz với gốc O trùng với điểm A, trục Ox trùng với cạnh AB, trục Oy trùng với cạnh AD, và trục Oz trùng với đường thẳng SA. Khi đó, ta có các tọa độ:
- A(0; 0; 0)
- B(a; 0; 0)
- C(a; a; 0)
- D(0; a; 0)
- S(0; 0; a)
Vectơ SC = (a; a; -a). Vectơ pháp tuyến của mặt phẳng (ABCD) là n = (0; 0; 1).
sin(θ) = |(a; a; -a) . (0; 0; 1)| / (√(a2 + a2 + (-a)2) * √(02 + 02 + 12)) = | -a | / (√(3a2) * 1) = a / (a√3) = 1/√3.
Vậy, θ = arcsin(1/√3) ≈ 35.26°.
Lưu Ý Quan Trọng
- Luôn kiểm tra lại các phép tính để đảm bảo tính chính xác.
- Hiểu rõ bản chất của bài toán trước khi bắt đầu giải.
- Sử dụng các công thức và định lý một cách chính xác.
Các Bài Tập Tương Tự
Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao. tusach.vn cũng cung cấp giải pháp cho nhiều bài tập khác, hãy truy cập để tìm hiểu thêm.
Kết Luận
Câu 44 trang 75 SGK Hình học 11 Nâng cao là một bài tập điển hình về ứng dụng của vectơ và phương trình trong không gian. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp bạn tự tin hơn trong các kỳ thi và bài kiểm tra.
Hy vọng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài toán. Chúc bạn học tốt!