Câu 27 trang 60 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Hình Học 11 Nâng Cao - Câu 27 Trang 60
Câu 27 trang 60 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và phương pháp giải bài tập.
Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?
Đề bài
Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?
Lời giải chi tiết
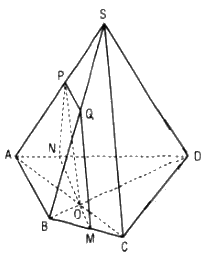
Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.
Giải Chi Tiết Câu 27 Trang 60 SGK Hình Học 11 Nâng Cao
Câu 27 trang 60 SGK Hình học 11 Nâng cao thường liên quan đến việc xác định mối quan hệ giữa các vectơ, kiểm tra tính đồng phẳng của ba vectơ, hoặc tìm giao điểm của đường thẳng và mặt phẳng. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng.
- Đường thẳng trong không gian: Phương trình tham số, phương trình chính tắc, vị trí tương đối giữa hai đường thẳng.
- Mặt phẳng trong không gian: Phương trình mặt phẳng, vectơ pháp tuyến, vị trí tương đối giữa đường thẳng và mặt phẳng.
- Kiểm tra tính đồng phẳng của ba vectơ: Sử dụng tích hỗn hợp.
Phân Tích Bài Toán và Phương Pháp Giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Sau đó, phân tích các dữ kiện đã cho và tìm ra mối liên hệ giữa chúng. Dựa vào đó, lựa chọn phương pháp giải phù hợp.
Thông thường, để giải Câu 27 trang 60, bạn có thể áp dụng các bước sau:
- Bước 1: Biểu diễn các vectơ liên quan theo các vectơ cơ sở.
- Bước 2: Sử dụng các phép toán trên vectơ để đơn giản hóa biểu thức.
- Bước 3: Áp dụng các công thức hoặc định lý liên quan để giải quyết bài toán.
- Bước 4: Kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví Dụ Minh Họa (Giả định một dạng bài tập phổ biến)
Đề bài: Cho bốn điểm A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6). Chứng minh rằng bốn điểm A, B, C, D đồng phẳng.
Giải:
Để chứng minh bốn điểm A, B, C, D đồng phẳng, ta cần chứng minh rằng ba vectơ AB, AC, AD đồng phẳng. Điều này tương đương với việc tích hỗn hợp của ba vectơ này bằng 0.
AB = (2-1; 3-2; 4-3) = (1; 1; 1)
AC = (3-1; 4-2; 5-3) = (2; 2; 2)
AD = (4-1; 5-2; 6-3) = (3; 3; 3)
Tích hỗn hợp AB . (AC x AD) = AB . (0; 0; 0) = 0
Vậy, bốn điểm A, B, C, D đồng phẳng.
Lưu Ý Quan Trọng
Khi giải các bài tập về vectơ, hãy chú ý đến việc sử dụng đúng các phép toán và công thức. Đồng thời, hãy kiểm tra lại kết quả để đảm bảo tính chính xác. Việc vẽ hình minh họa cũng có thể giúp bạn hiểu rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
Tusach.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ tự tin hơn khi giải Câu 27 trang 60 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các em học tốt!
| Khái niệm | Giải thích |
|---|---|
| Tích vô hướng | a.b = |a||b|cos(θ), dùng để tính góc giữa hai vectơ. |
| Tích có hướng | a x b là một vectơ vuông góc với cả a và b. |
| Tích hỗn hợp | a.(b x c), dùng để kiểm tra tính đồng phẳng của ba vectơ. |