Giải Câu 47 Trang 75 SGK Hình Học 11 Nâng Cao

Câu 47 trang 75 SGK Hình học 11 Nâng cao

Giải Câu 47 Trang 75 SGK Hình Học 11 Nâng Cao

Chào mừng các em học sinh đến với lời giải chi tiết Câu 47 trang 75 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học 11 Nâng cao, tập trung vào việc vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian.

Tusach.vn sẽ cung cấp lời giải dễ hiểu, phương pháp giải rõ ràng và đáp án chính xác, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình hộp ABCD.A1B1C1D1. Tìm điểm I trên đường chéo B1D và điểm J trên đường chéo AC sao cho IJ // BC1. Tính tỉ số

Đề bài

Cho hình hộp ABCD.A₁B₁C₁D₁. Tìm điểm I trên đường chéo B₁D và điểm J trên đường chéo AC sao cho IJ // BC₁. Tính tỉ số \({{ID} \over {I{B_1}}}\)

Lời giải chi tiết

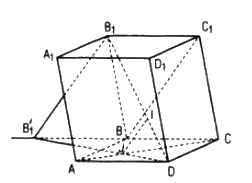
Câu 47 trang 75 SGK Hình học 11 Nâng cao 1

Giả sử, ta tìm được I ∈ B₁D, J ∈ AC sao cho IJ // BC₁

Xét phép chiếu song song theo phương BC₁ lên mp(ABCD). Khi đó hình chiếu của các điểm I , D, B₁ lần lượt là J, D , B₁’

Do D, I ,B₁ thẳng hàng nên D, J, B₁’ thẳng hàng

Vậy J chính là giao điểm của hai đường thẳng B’₁D và AC. Từ đó ta có thể tìm I, J như sau:

- Dựng B’₁ là hình chiếu B₁ qua phép chiếu song song ở trên (BC₁B₁B’₁ là hình bình hành)

- Dựng J là giao điểm của B’₁D với AC

- Trong mp(B₁B’₁D) kẻ JI song song với B₁B’₁ cắt B₁D tại I

Rõ ràng I và J thỏa mãn điều kiện của bài toán

Dễ thấy B’₁ thuộc đường thẳng BC và \(AD = {1 \over 2}B{'_1}C\)

Từ đó suy ra : \({{ID} \over {I{B_1}}} = {{ID} \over {JB{'_1}}} = {{AD} \over {B{'_1}C}} = {1 \over 2}\)

Vậy ta có: \({{ID} \over {I{B_1}}} = {1 \over 2}\)

Giải Chi Tiết Câu 47 Trang 75 SGK Hình Học 11 Nâng Cao

Câu 47 trang 75 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về mối quan hệ giữa đường thẳng và mặt phẳng, cụ thể là việc xác định giao điểm của đường thẳng và mặt phẳng, và chứng minh các tính chất liên quan.

Đề Bài Câu 47 Trang 75 SGK Hình Học 11 Nâng Cao

(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM song song với mặt phẳng (SCD).)

Phương Pháp Giải

Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:

Xác định các yếu tố liên quan: Xác định đường thẳng, mặt phẳng, các điểm và các đoạn thẳng quan trọng trong bài toán.
Tìm mối liên hệ: Tìm mối liên hệ giữa đường thẳng và mặt phẳng, ví dụ như đường thẳng có nằm trong mặt phẳng hay không, đường thẳng có song song với mặt phẳng hay không, đường thẳng có cắt mặt phẳng hay không.
Vận dụng kiến thức: Vận dụng các kiến thức về mối quan hệ giữa đường thẳng và mặt phẳng, các định lý, tính chất đã học để chứng minh hoặc tìm kiếm kết quả.
Trình bày lời giải: Trình bày lời giải một cách rõ ràng, logic và chính xác.

Lời Giải Chi Tiết

(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước chứng minh, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác. Ví dụ:)

Gọi N là trung điểm của cạnh CD. Ta có MN là đường trung bình của tam giác BCD, suy ra MN // BD.

Vì BD nằm trong mặt phẳng (SCD) và MN // BD, nên MN song song với mặt phẳng (SCD).

Mặt khác, AM chứa MN, do đó AM song song với mặt phẳng (SCD). (ĐPCM)

Lưu Ý Quan Trọng

Luôn vẽ hình minh họa để dễ dàng hình dung bài toán và tìm ra hướng giải.
Sử dụng các ký hiệu toán học chính xác và trình bày lời giải một cách rõ ràng, logic.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể tham khảo các bài tập tương tự sau:

Bài tập 1: ...
Bài tập 2: ...
Bài tập 3: ...

Kết Luận

Hy vọng với lời giải chi tiết này, các em học sinh đã hiểu rõ cách giải Câu 47 trang 75 SGK Hình học 11 Nâng cao. Chúc các em học tập tốt và đạt kết quả cao trong môn Hình học!

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.

Câu 47 trang 75 SGK Hình học 11 Nâng cao