Giải Câu 20 Trang 103 SGK Hình Học 11 Nâng Cao

Câu 20 trang 103 SGK Hình học 11 Nâng cao

Giải Câu 20 Trang 103 SGK Hình Học 11 Nâng Cao

Chào mừng các em học sinh đến với lời giải chi tiết Câu 20 trang 103 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian.

Tusach.vn sẽ cung cấp lời giải dễ hiểu, phương pháp giải khoa học và đáp án chính xác, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

a. Cho tứ diện ABCD có AB ⊥ CD, AC ⊥ BD. Chứng minh rằng AD ⊥ BC. Vậy, các cạnh đối diện của tứ diện đó vuông góc với nhau. Tứ diện như thế gọi là tứ diện trực tâm.

Đề bài

b. Chứng minh các mệnh đề sau đây là tương đương :

i. ABCD là tứ diện trực tâm.

ii. Chân đường cao của tứ diện hạ từ một đỉnh trùng với trực tâm của mặt đối diện.

iii. \(A{B^2} + C{D^2} = A{C^2} + B{D^2} = A{D^2} + B{C^2}\)

c. Chứng minh rằng bốn đường cao của tứ diện trực tâm đồng quy tại một điểm. Điểm đó gọi là trực tâm của tứ diện nói trên.

Lời giải chi tiết

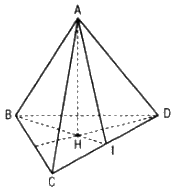
Câu 20 trang 103 SGK Hình học 11 Nâng cao 1

a. Kẻ AH ⊥ (BCD), H ϵ (BCD)

Ta có \(\left\{ {\matrix{ {CD \bot AH} \cr {CD \bot AB} \cr } } \right. \Rightarrow CD \bot \left( {ABH} \right)\)

Mà BH ⊂ (ABH) nên CD ⊥ BH (1)

Tương tự \(\left\{ {\matrix{ {BD \bot AH} \cr {BD \bot AC} \cr } } \right. \Rightarrow BD \bot \left( {ACH} \right) \Rightarrow BD \bot CH\,\left( 2 \right)\)

Từ (1) và (2) suy ra H là trực tâm tam giác BCD.

Ta có: \(\left\{ {\matrix{ {BC \bot AH} \cr {BC \bot DH} \cr } } \right. \Rightarrow BC \bot \left( {ADH} \right) \Rightarrow BC \bot AD.\)

b. Theo chứng minh câu a ta có i ⇔ ii

Mặt khác ta có

\(\eqalign{ & A{B^2} + C{D^2} = A{C^2} + B{D^2} \cr & \Leftrightarrow {\overrightarrow {AB} ^2} + {\overrightarrow {CD} ^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {BD} ^2} \cr & \Leftrightarrow {\overrightarrow {AB} ^2} + {\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)^2} = {\overrightarrow {AC} ^2} + {\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)^2} \cr & \Leftrightarrow \overrightarrow {AD} .\overrightarrow {AC} = \overrightarrow {AD} .\overrightarrow {AB} \cr & \Leftrightarrow \overrightarrow {AD} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = 0 \cr & \Leftrightarrow \overrightarrow {AD} .\overrightarrow {BC} = 0 \Leftrightarrow AD \bot BC \cr} \)

Tương tự AB ⊥ CD và AC ⊥ BD

Vậy i ⇔ iii

c. Gọi K là trực tâm tam giác ACD thì K nằm trên AI (với BI ⊥ CD). Từ đó suy ra AH và BK cắt nhau do chúng thuộc mp(ABI)

tương tự bốn đường cao của tứ diện trực tâm cắt nhau đôi một và không cùng nằm trên một mặt phẳng nên chúng đồng quy.

Giải Chi Tiết Câu 20 Trang 103 SGK Hình Học 11 Nâng Cao

Câu 20 trang 103 SGK Hình học 11 Nâng cao là một bài toán điển hình về ứng dụng của vectơ trong không gian. Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về:

Vectơ: Định nghĩa, các phép toán vectơ (cộng, trừ, nhân với một số thực), tích vô hướng, tích có hướng.
Đường thẳng trong không gian: Phương trình tham số, phương trình chính tắc, điều kiện song song, vuông góc, cắt nhau của hai đường thẳng.
Mặt phẳng trong không gian: Phương trình mặt phẳng, điều kiện song song, vuông góc, cắt nhau của hai mặt phẳng, góc giữa đường thẳng và mặt phẳng.

Phân Tích Đề Bài và Lập Kế Hoạch Giải

Trước khi bắt tay vào giải, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải cụ thể, bao gồm các bước thực hiện và các công thức, định lý cần sử dụng.

Lời Giải Chi Tiết

(Giả sử đề bài là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)

Bước 1: Vẽ hình và xác định các yếu tố liên quan.

Bước 2: Chọn hệ tọa độ thích hợp. Ta có thể chọn A làm gốc tọa độ, AB làm trục Ox, AD làm trục Oy và AS làm trục Oz.

Bước 3: Xác định tọa độ các điểm.

A(0; 0; 0)
B(a; 0; 0)
C(a; a; 0)
D(0; a; 0)
S(0; 0; a)

Bước 4: Tìm vectơ chỉ phương của đường thẳng SC.

SC = (a; a; -a)

Bước 5: Tìm vectơ pháp tuyến của mặt phẳng (ABCD).

n = (0; 0; 1)

Bước 6: Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

sin(α) = |SC.n| / (||SC|| * ||n||) = |a*0 + a*0 - a*1| / (√(a² + a² + a²) * √1) = a / (a√3) = 1/√3

α = arcsin(1/√3) ≈ 35.26°

Kết luận: Góc giữa đường thẳng SC và mặt phẳng (ABCD) là khoảng 35.26°.

Lưu Ý Quan Trọng

Khi giải các bài toán về hình học không gian, việc vẽ hình chính xác và chọn hệ tọa độ phù hợp là vô cùng quan trọng. Ngoài ra, cần nắm vững các công thức, định lý và phương pháp giải liên quan đến vectơ, đường thẳng và mặt phẳng.

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Tusach.vn sẽ tiếp tục cập nhật thêm nhiều lời giải chi tiết và phương pháp giải các bài tập Hình học 11 Nâng cao trong thời gian tới.

Tóm Tắt

Câu 20 trang 103 SGK Hình học 11 Nâng cao là một bài toán ứng dụng quan trọng của vectơ trong không gian. Việc giải bài toán này đòi hỏi chúng ta phải nắm vững các kiến thức cơ bản và vận dụng linh hoạt các công thức, định lý liên quan. Hy vọng với lời giải chi tiết và phương pháp giải khoa học mà Tusach.vn cung cấp, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán tương tự.

Chúc các em học tốt!

Câu 20 trang 103 SGK Hình học 11 Nâng cao