Giải Câu 7 Trang 121 SGK Hình Học 11 Nâng Cao

Câu 7 trang 121 SGK Hình học 11 Nâng cao

Giải Câu 7 Trang 121 SGK Hình Học 11 Nâng Cao

Chào mừng các em học sinh đến với lời giải chi tiết Câu 7 trang 121 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học 11 Nâng cao, tập trung vào việc rèn luyện kỹ năng giải toán về vectơ và ứng dụng trong hình học.

tusach.vn sẽ cung cấp đáp án chính xác, phương pháp giải dễ hiểu và các lưu ý quan trọng để giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :

Đề bài

Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :

a. Tứ diện ABCD là gần đều ;

b. Các đoạn thẳng nối trung điểm cặp cạnh đối diện đôi một vuông góc với nhau ;

c. Các trọng tuyến (đoạn thẳng nối đỉnh với trọng tâm của mặt đối diện) bằng nhau ;

d. Tổng các góc tại mỗi đỉnh bằng 180˚

Lời giải chi tiết

* Chứng minh a ⇔ b

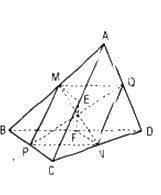
Câu 7 trang 121 SGK Hình học 11 Nâng cao 1

Gọi M, N, P, Q, E, F lần lượt là trung điểm của AB, CD, BC, AD, AC, BD.

a ⇒ b. Do AC = BD nên MNPQ là hình thoi, vì thế MN ⊥ PQ. Tương tự ta có MN ⊥ EF, PQ ⊥ EF.

b) ⇒ a. MPNQ là hình bình hành mà MN ⊥ PQ nên MPNQ là hình thoi, tức là MP = MQ, từ đó AC = BD.

Tương tự như trên, ta cũng có BC = AD, AB = CD.

* Chứng minh a ⇔ c

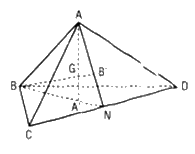
Câu 7 trang 121 SGK Hình học 11 Nâng cao 2

Gọi A’, B’ lần lượt là trọng tâm của các tam giác BCD và ACD.

a) ⇒ c. Ta có ΔBCD = ΔADC (c.c.c) nên BN = AN, từ đó A’N = B’N.

Vậy ΔAA’N = ΔBB’N (c.g.c), suy ra AA’ = BB’.

Tương tự như trên, ta có điều phải chứng minh.

c) ⇒ a. Do giả thiết ta có BB’ = AA’, mà AA’ cắt BB’ tại G, AG = 3GA’, BG = 3GB’ (xem BT 22, chương II, SGK), từ đó BG = AG và GA’ = GB’. Các tam giác BGA’ và AGB’ bằng nhau nên BA’ = AB’.

Như vậy BN = AN, mà :

\(\eqalign{ & A{C^2} + A{D^2} = 2A{N^2} + {{C{D^2}} \over 2} \cr & B{C^2} + B{D^2} = 2B{N^2} + {{C{D^2}} \over 2} \cr} \)

Do đó \(A{C^2} + A{D^2} = B{C^2} + B{D^2}\) (1)

Tương tự như trên ta có : \(C{A^2} + C{B^2} = D{A^2} + D{B^2}\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra AD = BC và AC = BD.

Tương tự như trên ta cũng có AB = CD.

* Chứng minh a ⇔ d

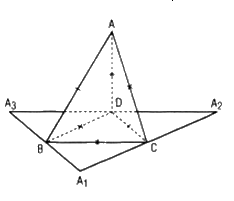
Câu 7 trang 121 SGK Hình học 11 Nâng cao 3

a) ⇒ d. Do sự bằng nhau của các tam giác ABC, CDA, BAD với tam giác DCB nên tổng các góc tại B bằng 180˚

Đối với các đỉnh còn lại cũng được lí luận tương tự như trên.

d) ⇒ a. Trải các mặt ABC, ACD, ABD lên mặt phẳng (BCD).

Do tổng các góc tại B cũng như tại C, tại D đều bằng 180˚ nên các bộ ba điểm A₁, C, A₂; A₂, D, A₃; A₃, B, A₁ là những bộ ba điểm thẳng hàng.

Như vậy, BC, CD, BD là ba đường trung bình của tam giác A₁A₂A₃. Từ đó BD = A₁C = CA₂ = CA. Tương tự ta cũng có AD = BC, CD = AB.

Giải Chi Tiết Câu 7 Trang 121 SGK Hình Học 11 Nâng Cao

Câu 7 trang 121 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực và tích vô hướng để giải quyết bài toán liên quan đến hình học phẳng.

Nội Dung Bài Toán

Thông thường, dạng bài tập này sẽ cho một hình vẽ (thường là tam giác, hình bình hành, hoặc các hình đa giác khác) và yêu cầu chứng minh một đẳng thức vectơ, tính độ dài một đoạn thẳng, hoặc xác định vị trí tương đối của các điểm.

Phương Pháp Giải

Phân tích bài toán: Đọc kỹ đề bài, xác định các yếu tố đã cho và yêu cầu cần tìm. Vẽ hình minh họa nếu cần thiết.
Chọn hệ tọa độ: Nếu bài toán liên quan đến tính toán, việc chọn hệ tọa độ thích hợp sẽ giúp đơn giản hóa quá trình giải.
Biểu diễn các vectơ: Sử dụng các vectơ để biểu diễn các đoạn thẳng, đường thẳng, và các yếu tố hình học khác.
Vận dụng các phép toán vectơ: Sử dụng các phép toán vectơ (cộng, trừ, nhân với một số thực, tích vô hướng) để biến đổi các biểu thức vectơ và chứng minh các đẳng thức.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví Dụ Minh Họa (Giả định nội dung câu 7)

Giả sử câu 7 có nội dung như sau: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2

Lời giải:

Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}
overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}
overrightarrow{AM} =overrightarrow{AC} +overrightarrow{CM} =overrightarrow{AC} -overrightarrow{MC}
Cộng hai phương trình trên, ta được: 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}
Suy ra: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm)

Lưu Ý Quan Trọng

Nắm vững các định nghĩa và tính chất của vectơ.
Thành thạo các phép toán vectơ.
Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Sử dụng hình vẽ minh họa để hiểu rõ bài toán.

Các Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. tusach.vn sẽ tiếp tục cập nhật lời giải chi tiết cho các bài tập còn lại trong chương trình Hình học 11 Nâng cao.

Tóm Tắt

Câu 7 trang 121 SGK Hình học 11 Nâng cao là một bài tập quan trọng giúp các em hiểu sâu hơn về vectơ và ứng dụng của nó trong hình học. Bằng cách nắm vững phương pháp giải và luyện tập thường xuyên, các em sẽ tự tin giải quyết các bài toán tương tự.

Chúc các em học tốt!

Câu 7 trang 121 SGK Hình học 11 Nâng cao