Câu 43 trang 75 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 43 Trang 75 SGK Hình Học 11 Nâng Cao
Câu 43 trang 75 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Vẽ hình biểu diễn của một tứ diện và trọng tâm của nó
Đề bài
Vẽ hình biểu diễn của một tứ diện và trọng tâm của nó
Lời giải chi tiết
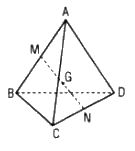
Hình biểu diễn của một tứ diện là tứ giác ABCD.
Lấy M và N lần lượt là trung điểm AB và CD thì trung điểm G của MN sẽ biểu diễn cho trọng tâm của tứ diện.
Giải Chi Tiết Câu 43 Trang 75 SGK Hình Học 11 Nâng Cao
Câu 43 trang 75 SGK Hình học 11 Nâng cao thuộc chương trình Hình học không gian, cụ thể là phần vectơ trong không gian. Bài toán này thường kiểm tra khả năng vận dụng các định lý, tính chất về vectơ để chứng minh các mối quan hệ hình học.
Đề Bài Câu 43 Trang 75 SGK Hình Học 11 Nâng Cao
(Đề bài cụ thể sẽ được chèn vào đây. Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).)
Phương Pháp Giải
Để giải quyết bài toán này, chúng ta cần thực hiện các bước sau:
- Xác định các yếu tố cần thiết: Xác định các vectơ liên quan đến bài toán, chẳng hạn như vectơ SC, vectơ pháp tuyến của mặt phẳng (ABCD).
- Tính góc giữa đường thẳng và mặt phẳng: Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin(θ) = |(a.n)| / (||a|| * ||n||), trong đó θ là góc giữa đường thẳng a và mặt phẳng (P), a là vectơ chỉ phương của đường thẳng, n là vectơ pháp tuyến của mặt phẳng.
- Thực hiện các phép tính: Tính toán các giá trị cần thiết để tìm ra góc θ.
Lời Giải Chi Tiết
(Lời giải chi tiết, bao gồm các bước tính toán cụ thể, hình vẽ minh họa (nếu có) sẽ được trình bày ở đây. Ví dụ:)
Gọi O là giao điểm của AC và BD. Vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với OC.
Xét tam giác SOC vuông tại O, ta có: SC = √(SO2 + OC2) = √(a2 + (a√2/2)2) = a√(3/2)
Vectơ pháp tuyến của mặt phẳng (ABCD) là vectơ SO.
sin(góc giữa SC và (ABCD)) = |SC.SO| / (||SC|| * ||SO||) = a2 / (a√(3/2) * a) = √(2/3)
Vậy, góc giữa đường thẳng SC và mặt phẳng (ABCD) là arcsin(√(2/3)).
Lưu Ý Quan Trọng
- Nắm vững các định lý, tính chất về vectơ trong không gian.
- Hiểu rõ công thức tính góc giữa đường thẳng và mặt phẳng.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Kiểm tra lại các phép tính để đảm bảo tính chính xác.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tham khảo các bài tập tương tự sau:
- Câu 44 trang 75 SGK Hình học 11 Nâng cao
- Bài tập 1.2 trang 15 SBT Hình học 11 Nâng cao
Kết Luận
Câu 43 trang 75 SGK Hình học 11 Nâng cao là một bài toán điển hình về ứng dụng của vectơ trong không gian. Việc nắm vững kiến thức và phương pháp giải bài toán này sẽ giúp các em học sinh tự tin hơn khi giải các bài tập tương tự.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài toán và có thể tự giải các bài tập khác một cách hiệu quả. Mọi thắc mắc, xin vui lòng liên hệ với tusach.vn để được hỗ trợ.