Câu 4 trang 9 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 4 Trang 9 SGK Hình Học 11 Nâng Cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 4 trang 9 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học không gian, tập trung vào việc vận dụng kiến thức về vectơ và các phép toán vectơ để giải quyết các bài toán thực tế.
Tusach.vn sẽ cung cấp lời giải dễ hiểu, phương pháp giải khoa học và đáp án chính xác, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Cho đường tròn (O) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm M’ sao cho
Đề bài
Cho đường tròn (O) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm M’ sao cho \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} .\)
Phương pháp giải - Xem chi tiết
Từ đẳng thức đã cho rút ra \(\overrightarrow {MM'} = \overrightarrow {AB} \) rồi nhận xét quỹ tích.
Lời giải chi tiết
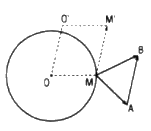
Ta có \(\overrightarrow {MM'} = \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {AB} \) nên phép tịnh tiến T theo vecto \(\overrightarrow {AB} \) biến M thành M’.
Do M nằm trên đường tròn (O;R) nên M' nằm trên đường tròn (O';R) là ảnh của (O;R) qua phép tịnh tiến T theo véc tơ \(\overrightarrow {AB} \).
Giải Chi Tiết Câu 4 Trang 9 SGK Hình Học 11 Nâng Cao
Câu 4 trang 9 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ để chứng minh một đẳng thức vectơ. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ.
Nội Dung Bài Toán
Bài toán thường có dạng: Cho các điểm A, B, C, D. Chứng minh rằng vectơ AB = vectơ CD hoặc một đẳng thức vectơ tương tự. Để giải bài toán này, chúng ta có thể sử dụng các phương pháp sau:
- Phương pháp hình học: Vẽ hình, xác định vị trí các điểm và sử dụng các tính chất của hình học để chứng minh đẳng thức vectơ.
- Phương pháp tọa độ: Chọn hệ tọa độ thích hợp, xác định tọa độ của các điểm và sử dụng các công thức tính vectơ để chứng minh đẳng thức vectơ.
- Sử dụng các tính chất của vectơ: Áp dụng các tính chất của vectơ như quy tắc cộng, trừ, nhân vectơ với một số thực, tính chất giao hoán, kết hợp, phân phối để biến đổi đẳng thức vectơ.
Lời Giải Chi Tiết
Để minh họa, giả sử bài toán yêu cầu chứng minh rằng với hình bình hành ABCD, ta có vectơ AB = vectơ DC.
- Phân tích: Trong hình bình hành ABCD, các cạnh đối song song và bằng nhau. Do đó, vectơ AB và vectơ DC là hai vectơ bằng nhau.
- Chứng minh:
Vì ABCD là hình bình hành nên AB // DC và AB = DC.
Suy ra, vectơ AB = vectơ DC (do hai vectơ cùng hướng và có độ dài bằng nhau).
Ví Dụ Minh Họa
Xét hình bình hành ABCD với A(0;0), B(2;0), C(3;1), D(1;1). Ta có:
- Vectơ AB = (2-0; 0-0) = (2;0)
- Vectơ DC = (1-3; 1-1) = (-2;0)
Tuy nhiên, trong ví dụ này, vectơ AB = - vectơ DC. Điều này cho thấy việc xác định hướng của vectơ là rất quan trọng. Trong trường hợp này, ta có thể nói vectơ AB và vectơ DC đối nhau.
Lưu Ý Quan Trọng
Khi giải các bài toán về vectơ, cần chú ý các điểm sau:
- Xác định đúng hướng của vectơ.
- Sử dụng đúng các quy tắc và tính chất của vectơ.
- Vẽ hình để minh họa và kiểm tra lại kết quả.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Cho hình vuông ABCD. Chứng minh rằng vectơ AB = vectơ DC và vectơ AD = vectơ BC.
- Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng vectơ AM = (1/2)(vectơ AB + vectơ AC).
Kết Luận
Câu 4 trang 9 SGK Hình học 11 Nâng cao là một bài tập cơ bản về vectơ, giúp các em làm quen với các khái niệm và tính chất của vectơ. Việc nắm vững kiến thức này là rất quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Hình học không gian.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Độ dài vectơ | Khoảng cách giữa điểm đầu và điểm cuối của vectơ. |
| Vectơ bằng nhau | Hai vectơ có cùng độ dài và cùng hướng. |
| Hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về Câu 4 trang 9 SGK Hình học 11 Nâng cao. Chúc các em học tốt! | |