Câu 11 trang 50 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 11 Trang 50 SGK Hình Học 11 Nâng Cao
Chào các em học sinh! Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho Câu 11 trang 50 sách giáo khoa Hình học 11 Nâng cao. Chúng tôi sẽ trình bày phương pháp giải, các bước thực hiện và đáp án chính xác để giúp các em nắm vững kiến thức và tự tin làm bài tập.
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
Đề bài
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)
Lời giải chi tiết
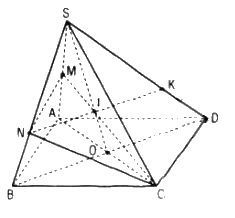
a. Tìm SO ∩ (CNM)
Trong mặt phẳng (SAC) gọi I là giao điểm của SO với CM
I = SO ∩ CM
\( \Rightarrow \left\{ \begin{array}{l}I \in SO\\I \in CM\end{array} \right.\)
mà CM ⊂ (CMN) nên I = SO ∩ (CMN)
b. Tìm (SAD) ∩ (CMN)
Trong mp(SBD) gọi K là giao điểm của NI và SD
K = NI ∩ SD
\( \Rightarrow \left\{ \begin{array}{l}K \in NI \subset \left( {CMN} \right)\\K \in SD \subset \left( {SAD} \right)\end{array} \right. \)\(\Rightarrow K \in \left( {CMN} \right) \cap \left( {SAD} \right)\)
Mà \(M \in \left( {SAD} \right) \cap \left( {CMN} \right)\)
Do đó (SAD) ∩ (CMN) = MK
Giải Chi Tiết Câu 11 Trang 50 SGK Hình Học 11 Nâng Cao
Câu 11 trang 50 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ như cộng, trừ, nhân với một số thực và tích vô hướng để giải quyết bài toán liên quan đến hình học phẳng. Bài toán thường xoay quanh việc chứng minh các đẳng thức vectơ, tính độ dài vectơ, hoặc xác định mối quan hệ giữa các vectơ.
Nội Dung Bài Toán (Ví dụ):
Giả sử bài toán yêu cầu chứng minh rằng với tam giác ABC, nếu M là trung điểm của BC thì 2AM = AB + AC. Đây là một bài toán điển hình để áp dụng quy tắc trung điểm và các phép toán vectơ.
Phương Pháp Giải
- Phân tích bài toán: Xác định rõ các vectơ cần làm việc và mối quan hệ giữa chúng.
- Sử dụng quy tắc trung điểm: Nếu M là trung điểm của BC, thì BM = MC và AM = AB + BM hoặc AM = AC + CM.
- Biến đổi vectơ: Sử dụng các phép toán vectơ để biến đổi biểu thức cần chứng minh về dạng đơn giản hơn.
- Kết luận: So sánh kết quả thu được với biểu thức ban đầu để đưa ra kết luận.
Lời Giải Chi Tiết (Ví dụ):
Ta có: AM = AB + BM. Vì M là trung điểm của BC nên BM = MC. Mà BC = AC - AB (hoặc BC = AB - AC tùy thuộc vào vị trí của các điểm). Do đó, BM = (AC - AB)/2.
Thay vào biểu thức của AM, ta được: AM = AB + (AC - AB)/2 = (2AB + AC - AB)/2 = (AB + AC)/2. Nhân cả hai vế với 2, ta có: 2AM = AB + AC (đpcm).
Các Dạng Bài Tập Tương Tự
- Chứng minh đẳng thức vectơ liên quan đến trung điểm, trọng tâm, đường phân giác, đường cao của tam giác.
- Tính độ dài của vectơ khi biết tọa độ các điểm.
- Xác định mối quan hệ giữa các vectơ để chứng minh các điểm thẳng hàng, song song, vuông góc.
Mẹo Giải Bài Tập Vectơ
Để giải tốt các bài tập về vectơ, các em cần:
- Nắm vững các định nghĩa, tính chất và các phép toán vectơ.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Sử dụng các công thức và quy tắc một cách linh hoạt.
Tóm Tắt
Câu 11 trang 50 SGK Hình học 11 Nâng cao là một bài tập quan trọng để rèn luyện kỹ năng vận dụng kiến thức về vectơ trong hình học phẳng. Bằng cách nắm vững phương pháp giải và luyện tập thường xuyên, các em sẽ tự tin giải quyết các bài toán tương tự một cách hiệu quả.
Bảng Tham Khảo (Ví dụ về các công thức liên quan)
| Công Thức | Mô Tả |
|---|---|
| AB + BC = AC | Quy tắc cộng vectơ |
| k(AB) = kAB | Quy tắc nhân vectơ với một số thực |
| AB.AC = |AB||AC|cos(θ) | Công thức tính tích vô hướng |
Hy vọng bài giải này sẽ giúp ích cho các em trong quá trình học tập. Chúc các em học tốt!