Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 57 Trang 93
Câu 57 trang 93 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi đồ thị để giải quyết.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
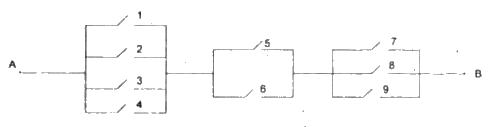
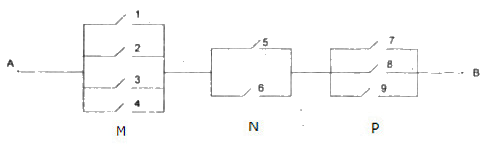
Xét hồ sơ mạng điện có 9 công tắc, trong đó mỗi công tắc có hai trạng thái đóng và mở.
Giải Chi Tiết Câu 57 Trang 93 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 57 trang 93 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến việc xét tính đơn điệu của hàm số, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hoặc tập xác định. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:
- Đạo hàm của hàm số: Hiểu rõ cách tính đạo hàm của các hàm số cơ bản và các quy tắc tính đạo hàm.
- Tính đơn điệu của hàm số: Biết cách xác định khoảng đồng biến, nghịch biến của hàm số dựa vào dấu của đạo hàm.
- Cực trị của hàm số: Nắm vững các bước tìm cực đại, cực tiểu của hàm số.
- Ứng dụng của đạo hàm: Sử dụng đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu, cực trị và các bài toán thực tế.
Phân tích bài toán và phương pháp giải
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, lựa chọn phương pháp giải phù hợp. Thông thường, để giải Câu 57 trang 93, học sinh sẽ thực hiện các bước sau:
- Tính đạo hàm f'(x) của hàm số f(x).
- Xác định các điểm tới hạn (điểm mà f'(x) = 0 hoặc f'(x) không xác định).
- Lập bảng biến thiên của hàm số f(x) để xác định khoảng đồng biến, nghịch biến và cực trị.
- Dựa vào bảng biến thiên để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên khoảng hoặc tập xác định cho trước.
Ví dụ minh họa (Giả sử đề bài cụ thể là tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên đoạn [-1; 3])
Bước 1: Tính đạo hàm
f'(x) = 3x2 - 6x
Bước 2: Tìm điểm tới hạn
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm tới hạn.
Bước 3: Lập bảng biến thiên
| x | -∞ | 0 | 2 | +∞ |
|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 4: Tìm giá trị lớn nhất và nhỏ nhất
f(-1) = (-1)3 - 3(-1)2 + 2 = -2
f(0) = 03 - 3(0)2 + 2 = 2
f(2) = 23 - 3(2)2 + 2 = -2
f(3) = 33 - 3(3)2 + 2 = 2
Vậy, giá trị lớn nhất của hàm số trên đoạn [-1; 3] là 2 (tại x = 0 và x = 3) và giá trị nhỏ nhất là -2 (tại x = -1 và x = 2).
Lưu ý khi giải bài tập
- Luôn kiểm tra điều kiện xác định của hàm số.
- Sử dụng đạo hàm cấp hai để xác định bản chất của điểm tới hạn (cực đại, cực tiểu).
- Vẽ đồ thị hàm số để kiểm tra lại kết quả.
Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các bạn học sinh sẽ tự tin giải quyết Câu 57 trang 93 SGK Đại số và Giải tích 11 Nâng cao và các bài tập tương tự. Chúc các bạn học tốt!